ЬтФПФкШн
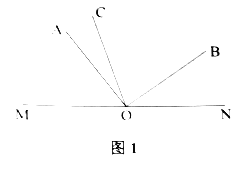
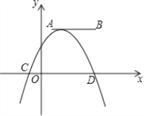
ЁОЬтФПЁПЃЈ1ЃЉВйзїЫМПМЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕШбќжБНЧ![]() ЕФжБНЧЖЅЕу
ЕФжБНЧЖЅЕу![]() дкдЕуЃЌНЋЦфШЦзХЕу
дкдЕуЃЌНЋЦфШЦзХЕу![]() а§зЊЃЌШєЖЅЕу
а§зЊЃЌШєЖЅЕу![]() ЧЁКУТфдкЕу
ЧЁКУТфдкЕу![]() ДІЃЎдђЂй
ДІЃЎдђЂй![]() ЕФГЄЮЊ______ЃЛЂкЕу
ЕФГЄЮЊ______ЃЛЂкЕу![]() ЕФзјБъЮЊ______ЃЈжБНгаДНсЙћЃЉ
ЕФзјБъЮЊ______ЃЈжБНгаДНсЙћЃЉ
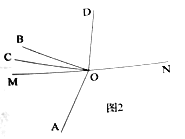
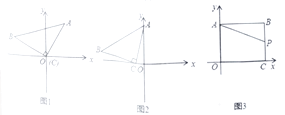
ЃЈ2ЃЉИаЮђгІгУЃКШчЭМ2ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕШбќжБНЧ![]() ШчЭМЗХжУЃЌжБНЧЖЅЕу
ШчЭМЗХжУЃЌжБНЧЖЅЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌЪдЧѓжБЯп
ЃЌЪдЧѓжБЯп![]() ЕФКЏЪ§БэДяЪНЃЎ
ЕФКЏЪ§БэДяЪНЃЎ
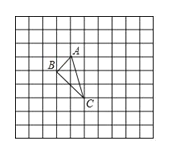
ЃЈ3ЃЉЭиеЙбаОПЃКШчЭМ3ЃЌдкжБНЧзјБъЯЕжаЃЌЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЃЌзї
ЃЌзї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЌЕу
ЩЯЕФвЛИіЖЏЕуЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЖЏЕуЃЎЮЪЪЧЗёДцдквдЕу
ЩЯвЛЖЏЕуЃЎЮЪЪЧЗёДцдквдЕу![]() ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧ
ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧ![]() ЃЌШєДцдкЃЌЧыжБНгаДГіДЫЪБ
ЃЌШєДцдкЃЌЧыжБНгаДГіДЫЪБ![]() ЕуЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕуЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙДЙЩЖЈРэПЩЕУOAГЄЃЌгЩ![]() ЖдгІБпЯрЕШПЩЕУBЕузјБъЃЛ
ЖдгІБпЯрЕШПЩЕУBЕузјБъЃЛ
ЃЈ2ЃЉЭЈЙ§жЄУї![]() ЕУГіЕуBзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯп
ЕУГіЕуBзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
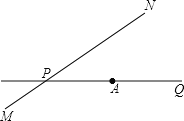
ЃЈ3ЃЉЩшЕуQзјБъЮЊ![]() ЃЌПЩЭЈЙ§жЄШ§НЧаЮШЋЕШЕФаджЪПЩЕУaЕФжЕЃЌгЩQЕузјБъПЩМфНгЧѓГіPЕузјБъ.
ЃЌПЩЭЈЙ§жЄШ§НЧаЮШЋЕШЕФаджЪПЩЕУaЕФжЕЃЌгЩQЕузјБъПЩМфНгЧѓГіPЕузјБъ.
НтЃКЃЈ1ЃЉШчЭМ1ЃЌзї![]() жсгкFЃЌ
жсгкFЃЌ![]() жсгкE.
жсгкE.
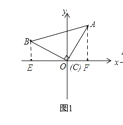
гЩAЕузјБъПЩжЊ![]()
дк![]() жаЃЌИљОнЙДЙЩЖЈРэПЩЕУ
жаЃЌИљОнЙДЙЩЖЈРэПЩЕУ![]() ЃЛ
ЃЛ
![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()
![]()
![]() жсгкFЃЌ
жсгкFЃЌ![]() жсгкE
жсгкE
![]()
гж![]()
![]()
![]()
![]()
ЫљвдBЕузјБъЮЊЃК![]()
ЃЈ2ЃЉШчЭМЃЌЙ§Еу![]() зї
зї![]() жсЃЎ
жсЃЎ
![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()
![]()
![]() жс
жс
![]()
гж![]()
![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]()
Ёр![]() ЃЎ
ЃЎ
ЩшжБЯп![]() ЕФБэДяЪНЮЊ
ЕФБэДяЪНЮЊ![]()
НЋ![]() КЭ
КЭ![]() ДњШыЃЌЕУ
ДњШыЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЕФКЏЪ§БэДяЪН
ЕФКЏЪ§БэДяЪН![]() ЃЎ
ЃЎ
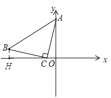
ЃЈ3ЃЉШчЭМ3ЃЌЗжСНжжЧщПіЃЌЕуQПЩдкxжсЯТЗНКЭЕуQдкxжсЩЯЗН
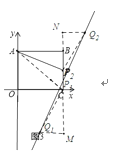
ЩшЕуQзјБъЮЊ![]() ЃЌЕуPзјБъЮЊ
ЃЌЕуPзјБъЮЊ![]()
ЕБЕуQдкxжсЯТЗНЪБЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛЦфбгГЄЯпгкMЃЌдђMЕузјБъЮЊ
НЛЦфбгГЄЯпгкMЃЌдђMЕузјБъЮЊ![]()
![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()
![]()
![]()
![]()
гж![]()
![]()
![]()
![]()
гЩЬтвтЕУ![]()
![]() ЃЌ
ЃЌ![]()
НтЕУ![]() ЃЌЫљвд
ЃЌЫљвд![]()
ЕБЕуQдкxжсЩЯЗНЪБЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛЦфбгГЄЯпгкNЃЌдђNЕузјБъЮЊ
НЛЦфбгГЄЯпгкNЃЌдђNЕузјБъЮЊ![]()
ЭЌРэПЩЕУ![]() ,
,![]()
гЩЬтвтЕУ![]()
![]() ЃЌ
ЃЌ![]()
НтЕУ![]() ЃЌЫљвд
ЃЌЫљвд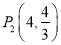
злЩЯ![]() ЕФзјБъЮЊЃК
ЕФзјБъЮЊЃК![]() ЃЎ
ЃЎ