题目内容
抛物线y=3（x-2）2-3的顶点坐标为________，对称轴是________． y=3x2先向________平移________个单位．再向________平移________个单位得到．
（2，-3） x=2 右 2 下 3
分析：先根据二次函数的顶点式得出此函数的顶点坐标及对称轴；再由函数图象平移的法则即可得出结论．
解答：∵抛物线的解析式为：y=3（x-2）2-3，
∴其顶点坐标为（2，-3），对称轴为x=2；
由“左加右减，上加下减”的原则可知，抛物线y=3x2先向右平移2各单位，再向下平移3个单位即可得到抛物线y=3（x-2）2-3．
故答案案为：（2，-3），x=2，右，2，下，3．
点评：本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
分析：先根据二次函数的顶点式得出此函数的顶点坐标及对称轴；再由函数图象平移的法则即可得出结论．
解答：∵抛物线的解析式为：y=3（x-2）2-3，
∴其顶点坐标为（2，-3），对称轴为x=2；
由“左加右减，上加下减”的原则可知，抛物线y=3x2先向右平移2各单位，再向下平移3个单位即可得到抛物线y=3（x-2）2-3．
故答案案为：（2，-3），x=2，右，2，下，3．
点评：本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
A和C，和x轴的另一个交点为B．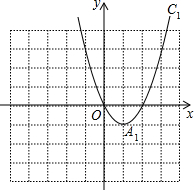
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．