题目内容
如图，点A的坐标为（－1，0），点B在直线y=2x－4上运动，当线段AB最短时，点B的坐标是（ ）
A．（－ ，－ ） | B．（，） | C．（－，） | D．（，－） |
D.
解析试题分析：设AB′解析式为y=kx+b，
∵AB′⊥BB′，BB′解析式为y=2x-4，k1×k2=-1，
∴2k=-1，k=-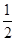
，
于是函数解析式为y=-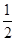x+b，
将A（-1，0）代入y=-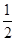x+b得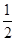，+b=0，b=-，
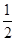则函数解析式为y=-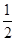x-，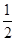
将两函数解析式组成方程组得，
，解得
，
故B点坐标为（，-）．
故选D.
考点: 1.一次函数的性质；2.垂线段最短．
练习册系列答案
相关题目
一次函数y=kx﹣k（k＜0）的图象大致是（ ）
A． | B． | C． | D． |
甲、乙两辆摩托车同时从相距20km的A，B两地出发，相向而行．图中l1，l2分别表示甲、乙两辆摩托车到A地的距离s（km）与行驶时间t（h）的函数关系．则下列说法错误的是（ ）
| A．乙摩托车的速度较快 |
| B．经过0.3小时甲摩托车行驶到A，B两地的中点 |
| C．经过0.25小时两摩托车相遇 |
D．当乙摩托车到达A地时，甲摩托车距离A地 km |
与
的图象交于A、B两点，过A作AC
轴于C,则
BOC的面积是（ ）．
的图象相交于点P，能表示这个一次函数图象的方程是（ ）
已知点(－4，y1)，(2， y2)都在直线y＝－
x＋2上，则y1与y2大小关系是 ( )
| A．y1＞y2 | B．y1＝y2 |
| C．y1＜y2 | D．不能比较 |