题目内容
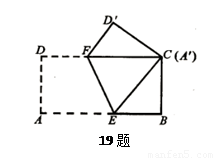
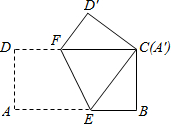 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则△CEB的面积为
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则△CEB的面积为6cm2
6cm2
.分析:利用翻折变换的性质得出AE=EC,进而利用勾股定理求出即可.
解答: 解:∵将长8cm,宽4cm的矩形纸片ABCD折叠,设BE=x,
解:∵将长8cm,宽4cm的矩形纸片ABCD折叠,设BE=x,
∴EC=8-x,
∴EC2=EB2+BC2,
∴(8-x)2=x2+16,
解得:x=3,
∴△CEB的面积为:
×EB×BC=
×3×4=6cm2.
故答案为:6cm2.
 解:∵将长8cm,宽4cm的矩形纸片ABCD折叠,设BE=x,
解:∵将长8cm,宽4cm的矩形纸片ABCD折叠,设BE=x,∴EC=8-x,
∴EC2=EB2+BC2,
∴(8-x)2=x2+16,
解得:x=3,
∴△CEB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:6cm2.
点评:此题主要考查了翻折变换的性质以及勾股定理的应用,利用已知得出AE=EC进而求出是解题关键.

练习册系列答案
相关题目
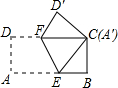 如图,将长8cm、宽4cm的矩形纸片ABCD折叠,使点A与C重合,则FC的长等于( )
如图,将长8cm、宽4cm的矩形纸片ABCD折叠,使点A与C重合,则FC的长等于( )