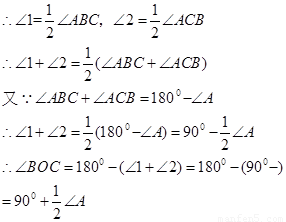题目内容
认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
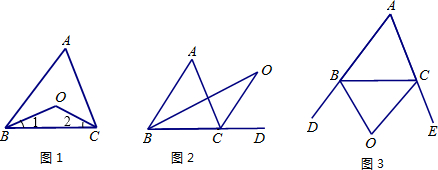
探究1:如图1,在 中,
中, 是
是 与
与 的平分线
的平分线 和
和 的交点,通过分析发现
的交点,通过分析发现 ,理由如下:
,理由如下:
∵ 和
和 分别是
分别是 和
和 的角平分线
的角平分线



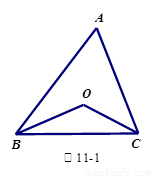
(1)探究2:如图2中,  是
是 与外角
与外角 的平分线
的平分线 和
和 的交点,试分析
的交点,试分析 与
与 有怎样的关系?请说明理由.
有怎样的关系?请说明理由.
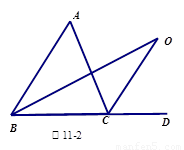
(2)探究3: 如图3中, 是外角
是外角 与外角
与外角 的平分线
的平分线 和
和 的交点,则
的交点,则 与
与 有怎样的关系?(直接写出结论)
有怎样的关系?(直接写出结论)
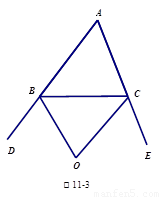
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

【答案】
解:
(1) 探究2结论:∠BOC=
理由如下:
∵ BO和CO分别是∠ABC和∠ACD的角平分线


(2) 探究3:结论∠BOC=90°-
(3) 拓展:结论
【解析】(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠O的关系;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.
(3)拓展:结论 .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
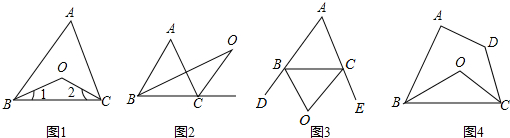


 中,
中, 是
是 与
与 的平分线
的平分线 和
和 的交点,分析发现
的交点,分析发现 ,理由如下: ∵
,理由如下: ∵


 的平分线
的平分线 与
与 有怎样的关系?请说明理由.
有怎样的关系?请说明理由. 与外角
与外角 的平分线
的平分线 ,理由如下:
,理由如下: