Question

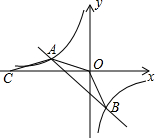（2013•吉安模拟）如图，直线AB与反比例函数的图象交于点A（-4，m）、B（2，n）两点，在x轴上取一点C，使OA=AC．
（1）如果OAC的面积为8，试确定反比例函数的表达式；
（2）求AB的长和cos∠OBA的值．

Answer 1

分析：（1）设反比例解析式为y=

k

x

，在三角形OAC中，OA=AC，过A作AD垂直于x轴，确定出CD=OD=4，OC=8，AD=m，表示出三角形OAC面积，根据三角形OAC面积为8求出m的值，确定出A坐标，进而求出k的值，确定出反比例解析式；
（2）由反比例解析式求出m与n的值，确定出A与B坐标，得到OA=OB，过O作OE垂直于AB，过B作BF垂直于y轴，由OA=OB得到E为AB中点，即AE=BE=

1

2

AB，求出OB与BE的长，即可确定出AB及cos∠ABO的值．

解答：解：（1）设反比例函数解析式为y=

k

x

，
在△OAC中，OA=AC，过A作AD⊥x轴，
∵点C在x轴的负半轴上，点A在第二象限，
∴CD=OD=4，OC=8，AD=m，
∴△OAC面积为

1

2

AD•OC=8=4m，即m=2，
∴k=-4×2=-8，
则反比例函数解析式为y=-

8

x

；

（2）反比例函数解析式为y=-

8

x

，即2n=-8，-4m=-8，
解得：m=2，n=-4，即A（-4，2），B（2，-4），
过点O作OE⊥AB于点E，BF⊥y轴于点F，
∵△AOD≌△BOF，
∴∠AOD=∠BOF，
∴sin∠AOD=sin∠BOF=

2

4

=

1

2

，OA=OB=

20

=2

5

，
∴BE=AE=

1

2

AB=

1

2

×

62+62

=3

2

，
则AB=6

2

，cos∠ABO=

BE

OB

=

3 2

2 5

=

3 10

10

．

点评：此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法确定函数解析式，坐标与图形性质，锐角三角函数定义，熟练掌握待定系数法是解本题的关键．