Question

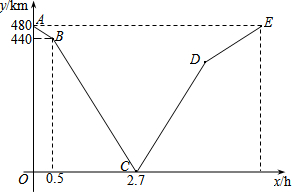
一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为x h，两车之间的距离为y km，图中的折线表示y与x之间的函数关系．根据图象解决以下问题：

（1）慢车的速度为   km/h，快车的速度为   km/h；

（2）解释图中点D的实际意义并求出点D的坐标；

（3）求快车出发多少时间时，两车之间的距离为300km？

 

Answer 1

【答案】

（1）80，120；（2）快车到达乙地，D（4.5，360）；（3）0.7或3.7小时

【解析】

试题分析：仔细分析图象特征根据路程、速度、时间的关系求解即可.

（1）(480－440)÷0.5=80，440 ÷2.2－80=120；

（2）快车到达乙地；    

因为快车走完全程所需时间为480÷120=4（h），所以点D的横坐标为4.5，纵坐标为200×1.8=360，即点D（4.5，360）；

（3）由题意，可知两车行驶的过程中有2次两车之间的距离为300km．

即(80＋120)×(x－0.5)=440－300，解得x=1.2（h），x-0.5=0.7(h)；

或(80＋120)×(x－2.7)=300，解得x=4.2（h）,x-0.5=3.7(h

故快车出发0.7或3.7小时时，两车之间的距离为300km．

考点：一次函数的应用

点评：一次函数的应用是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.