题目内容
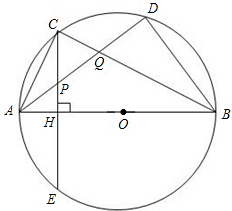（2012•泸州）如图，△ABC内接于⊙O，AB是⊙O的直径，C是弧AD的中点，弦CE⊥AB于点H，连接AD，分别交CE、BC于点P、Q，连接BD．（1）求证：P是线段AQ的中点；
（2）若⊙O的半径为5，AQ=
| 15 | 2 |
分析：（1）首先利用等角对等边证明：∠ACP=∠CAP得到：PA=PC，然再证明PC=PQ，即可得到P是AQ的中点；
（2）首先证明：△CAQ∽△CBA，依据相似三角形的对应边的比相等求得AC、BC的长度，然后根据直角三角形的面积公式即可求得CH的长，则可以求得CE的长．
（2）首先证明：△CAQ∽△CBA，依据相似三角形的对应边的比相等求得AC、BC的长度，然后根据直角三角形的面积公式即可求得CH的长，则可以求得CE的长．
解答：（1）证明：∵AB是⊙O的直径，弦CE⊥AB，
∴
=
．
又∵C是
的中点，
∴
=
，
∴
=
．
∴∠ACP=∠CAP．
∴PA=PC，
∵AB是直径．
∴∠ACB=90°．
∴∠PCQ=90°-∠ACP，∠CQP=90°-∠CAP，
∴∠PCQ=∠CQP．
∴PC=PQ．
∴PA=PQ，即P是AQ的中点；
（2）解：∵
=
，
∴∠CAQ=∠ABC．
又∵∠ACQ=∠BCA，
∴△CAQ∽△CBA．
∴
=
=
=
．
又∵AB=10，
∴AC=6，BC=8．
根据直角三角形的面积公式，得：AC•BC=AB•CH，
∴6×8=10CH．
∴CH=
．
又∵CH=HE，
∴CE=2CH=
．
∴
 |
| AC |
|
| AE |
又∵C是
|
| AD |
∴
|
| AC |
|
| CD |
∴
|
| AE |
|
| CD |
∴∠ACP=∠CAP．
∴PA=PC，
∵AB是直径．
∴∠ACB=90°．
∴∠PCQ=90°-∠ACP，∠CQP=90°-∠CAP，
∴∠PCQ=∠CQP．
∴PC=PQ．
∴PA=PQ，即P是AQ的中点；
（2）解：∵
|
| AC |
|
| CD |
∴∠CAQ=∠ABC．
又∵∠ACQ=∠BCA，
∴△CAQ∽△CBA．
∴
| AC |
| BC |
| AQ |
| AB |
| ||
| 10 |
| 3 |
| 4 |
又∵AB=10，
∴AC=6，BC=8．
根据直角三角形的面积公式，得：AC•BC=AB•CH，
∴6×8=10CH．
∴CH=
| 24 |
| 5 |
又∵CH=HE，
∴CE=2CH=
| 48 |
| 5 |
点评：本题考查了圆周角定理以及相似三角形的判定与性质，三角形的面积公式，正确理解定理是关键．
练习册系列答案
名校课堂系列答案
相关题目
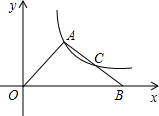（2012•泸州）如图，在△OAB中，C是AB的中点，反比例函数y=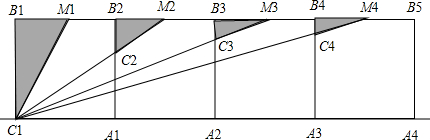
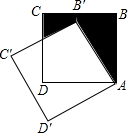（2012•泸州）如图，边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′，图中阴影部分的面积为（ ）
（2012•泸州）如图，矩形ABCD中，E是BC的中点，连接AE，过点E作EF⊥AE交DC于点F，连接AF．设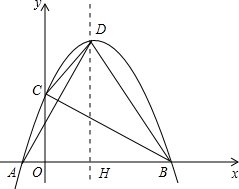
侧），与y轴相交于点C，顶点D在第一象限．过点D作x轴的垂线，垂足为H．