题目内容
已知等腰△ABC的一边长c=3,另两边长a、b恰是关于x的方程x2-(2k+1)x+4(k- )=0的两个根,求△ABC的周长.
)=0的两个根,求△ABC的周长.
解:(1)若c为底边,则a=b,故原方程有两个相等的实数根,
则[-(2k+1)]2-4×4(k- )=0,
)=0,
k= ,
,
当k= 时,原方程为x2-4x+4=0
时,原方程为x2-4x+4=0
则x1=x2=2,即a=b=2,
∴△ABC的周长为7.
(2)若c=3为腰,可设a为底,则b=c=3
∵b为原方程的根,
所以将b=3代入原方程得32-3(2k+1)+4(k- )=0,
)=0,
解得:k=2,
当k=2时,原方程为x2-5x+6=0,
解得:x=2或3,
即a=2,b=3,
∴△ABC的周长为8.
分析:根据等腰三角形的性质分两种情况:①a=b,c=3;②b=c讨论解答即可.
点评:本题考查一元二次方程的应用,等腰三角形的周长应注意两种情况,以及两种情况的取舍.
则[-(2k+1)]2-4×4(k-
 )=0,
)=0,k=
 ,
,当k=
 时,原方程为x2-4x+4=0
时,原方程为x2-4x+4=0则x1=x2=2,即a=b=2,
∴△ABC的周长为7.
(2)若c=3为腰,可设a为底,则b=c=3
∵b为原方程的根,
所以将b=3代入原方程得32-3(2k+1)+4(k-
 )=0,
)=0,解得:k=2,
当k=2时,原方程为x2-5x+6=0,
解得:x=2或3,
即a=2,b=3,
∴△ABC的周长为8.
分析:根据等腰三角形的性质分两种情况:①a=b,c=3;②b=c讨论解答即可.
点评:本题考查一元二次方程的应用,等腰三角形的周长应注意两种情况,以及两种情况的取舍.

练习册系列答案
相关题目
已知等腰△ABC的周长为18cm,BC=8cm,若△ABC≌△A′B′C′,则△A′B′C′中一定有一条边等于( )
| A、7cm | B、2cm或7cm | C、5cm | D、2cm或5cm |
 如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )
如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )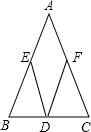 如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为
如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为