题目内容
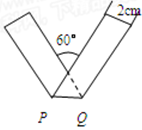
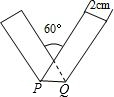 将宽为2cm的长方形纸条折叠成如图形状,则折痕的长是
将宽为2cm的长方形纸条折叠成如图形状,则折痕的长是分析:由平行线的性质可知∠BPD=∠BAC=60°,由折叠的性质可知∠DPQ+∠BPQ=180°,可推出∠APQ=60°,而∠PAQ=∠BAC=60°,可知△APQ为等边三角形,作QH⊥PA,则QH=2cm,解直角三角形可求折痕PQ.
解答: 解:如图,作QH⊥PA,垂足为H,则QH=2cm,
解:如图,作QH⊥PA,垂足为H,则QH=2cm,
由平行线的性质,得∠DPA=∠BAC=60°,
由折叠的性质,得∠DPQ+∠APQ=180°,
即∠DPA+∠APQ+∠APQ=180°,60°+2∠APQ=180°,
解得∠APQ=60°,又∠PAQ=∠BAC=60°,
∴△APQ为等边三角形,
在Rt△PQH中,sin∠HPQ=
,
∴PQ=
=
.
故答案为:
.
 解:如图,作QH⊥PA,垂足为H,则QH=2cm,
解:如图,作QH⊥PA,垂足为H,则QH=2cm,由平行线的性质,得∠DPA=∠BAC=60°,
由折叠的性质,得∠DPQ+∠APQ=180°,
即∠DPA+∠APQ+∠APQ=180°,60°+2∠APQ=180°,
解得∠APQ=60°,又∠PAQ=∠BAC=60°,
∴△APQ为等边三角形,
在Rt△PQH中,sin∠HPQ=
| HQ |
| PQ |
∴PQ=
| 2 |
| sin60° |
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题考查了折叠的性质,等边三角形的判定及解直角三角形的运用.关键是由已知推出等边三角形,用HQ表示纸条的宽.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
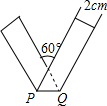 将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、2cm |
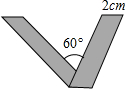 同学们在拍照留念的时候最喜欢做一个“V”字型的动作.我们将宽为2cm的长方形如图进行翻折,便可得到一个漂亮的“V”.如果“V”所成的锐角为60°,那么折痕AQ长是
同学们在拍照留念的时候最喜欢做一个“V”字型的动作.我们将宽为2cm的长方形如图进行翻折,便可得到一个漂亮的“V”.如果“V”所成的锐角为60°,那么折痕AQ长是 (2010•黔东南州)将宽为2cm的长方形折叠成如图所示的形状,那么折痕AB的长是( )
(2010•黔东南州)将宽为2cm的长方形折叠成如图所示的形状,那么折痕AB的长是( )