题目内容
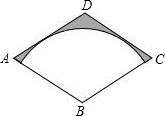（2013•桂林）如图，菱形ABCD的对角线BD、AC分别为2、2| 3 |
分析：连接AC、BD、BE，在Rt△AOB中可得∠BAO=30°，∠ABO=60°，在Rt△ABE中求出BE，得出扇形半径，由菱形面积减去扇形面积即可得出阴影部分的面积．
解答：解：连接AC、BD、BE，
∵四边形ABCD是菱形，
∴AC与BD互相垂直且平分，
∴AO=
，BO=1，
∵tan∠BAO=
，tan∠ABO=
，
∴∠BAO=30°，∠ABO=60°，
∴AB=2，∠BAE=60°，
∵以B为圆心的弧与AD相切，
∴∠AEB=90°，
在Rt△ABE中，AB=2，∠BAE=60°，
∴BE=ABsin60°=
，
∴S菱形-S扇形=
×2×2
-
=2
-π．
故选D．
∵四边形ABCD是菱形，
∴AC与BD互相垂直且平分，
∴AO=
| 3 |
∵tan∠BAO=
| ||
| 3 |
| 3 |
∴∠BAO=30°，∠ABO=60°，
∴AB=2，∠BAE=60°，
∵以B为圆心的弧与AD相切，
∴∠AEB=90°，
在Rt△ABE中，AB=2，∠BAE=60°，
∴BE=ABsin60°=
| 3 |
∴S菱形-S扇形=
| 1 |
| 2 |
| 3 |
120π×(
| ||
| 360 |
| 3 |
故选D．
点评：本题考查了扇形的面积计算、菱形的性质及切线的性质，解答本题的关键是根据菱形的性质求出各角度及扇形的半径．
练习册系列答案
阅读快车系列答案
相关题目
（2013•桂林）如图，与∠1是同位角的是（ ）
（2013•桂林）如图，在△ABC中，CA=CB，AD⊥BC，BE⊥AC，AB=5，AD=4，则AE=
（2013•桂林）如图，已知线段AB=10，AC=BD=2，点P是CD上一动点，分别以AP、PB为边向上、向下作正方形APEF和PHKB，设正方形对角线的交点分别为O1、O2，当点P从点C运动到点D时，线段O1O2中点G的运动路径的长是
（2013•桂林）如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．求证：
（2013•桂林）如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD交AB于E，以AE为直径作⊙O．