题目内容
 如图,等腰三角形ABC中,∠BAC=90°,在底边BC上截取BD=AB,过D作DE⊥BC交AC于E,连接AD,则图中等腰三角形的个数是
如图,等腰三角形ABC中,∠BAC=90°,在底边BC上截取BD=AB,过D作DE⊥BC交AC于E,连接AD,则图中等腰三角形的个数是
- A.1
- B.2
- C.3
- D.4
D
分析:三角形ABC是等腰三角形,且∠BAC=90°,所以∠B=∠C=45°,又DE⊥BC,所以∠DEC=∠C=45°,所以△EDC是等腰三角形,BD=AB,所以△ABD是等腰三角形,∠BAD=∠BDA,而∠EAD=90°-∠BAD,∠EDA=90°-∠BDA,所以∠EAD=∠EDA,所以△EAD是等腰三角形,因此图中等腰三角形共4个.
解答:∵三角形ABC是等腰三角形,且∠BAC=90°,
∴∠B=∠C=45°,
∵DE⊥BC,
∴∠EDB=∠EDC=90°
∴∠DEC=∠C=45°,
∴△EDC是等腰三角形,
∵BD=AB,
∴△ABD是等腰三角形,
∴∠BAD=∠BDA,
而∠EAD=90°-∠BAD,∠EDA=90°-∠BDA,
∴∠EAD=∠EDA,
∴△EAD是等腰三角形,
因此图中等腰三角形共4个.
故选D.
点评:本题考查了等腰三角形的性质和判定及三角形内角和定理;由已知条件利用相关的性质求得各个角的度数是正确解答本题的关键.
分析:三角形ABC是等腰三角形,且∠BAC=90°,所以∠B=∠C=45°,又DE⊥BC,所以∠DEC=∠C=45°,所以△EDC是等腰三角形,BD=AB,所以△ABD是等腰三角形,∠BAD=∠BDA,而∠EAD=90°-∠BAD,∠EDA=90°-∠BDA,所以∠EAD=∠EDA,所以△EAD是等腰三角形,因此图中等腰三角形共4个.
解答:∵三角形ABC是等腰三角形,且∠BAC=90°,
∴∠B=∠C=45°,
∵DE⊥BC,
∴∠EDB=∠EDC=90°
∴∠DEC=∠C=45°,
∴△EDC是等腰三角形,
∵BD=AB,
∴△ABD是等腰三角形,
∴∠BAD=∠BDA,
而∠EAD=90°-∠BAD,∠EDA=90°-∠BDA,
∴∠EAD=∠EDA,
∴△EAD是等腰三角形,
因此图中等腰三角形共4个.
故选D.
点评:本题考查了等腰三角形的性质和判定及三角形内角和定理;由已知条件利用相关的性质求得各个角的度数是正确解答本题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
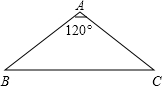 如图,等腰三角形ABC的顶角为120°,底边BC=
如图,等腰三角形ABC的顶角为120°,底边BC=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
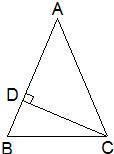 9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )
9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( ) (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?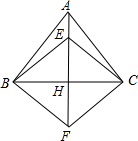 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH, 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转