题目内容
 (2012•松北区一模)王大爷要围成一个矩形花圃.花圃的一边利用20米长的墙,另三边用总长为36米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米,且BC>AB.矩形ABCD的面积为S平方米.
(2012•松北区一模)王大爷要围成一个矩形花圃.花圃的一边利用20米长的墙,另三边用总长为36米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米,且BC>AB.矩形ABCD的面积为S平方米.(1)求S与x之间的函数关系式(要求直接写出自变量x的取值范围);
(2)根据题中要求,所围花圃面积能否是154米2,若能,求出的x值; 若不能,请说明理由.
分析:(1)花圃的面积=AB×BC,根据BC比AB大,又不超过20可得自变量的取值范围;
(2)让(1)中的S=154求得合适的解即可.
(2)让(1)中的S=154求得合适的解即可.
解答:解:(1)由题意得BC=36-2x,
∴S=x(36-2x)=-2x2+36x.
,
解得8≤x<12
∴S=-2x2+36x(8≤x<12);
(2)-2x2+36x=154,
2x2-36x+154=0,
x2-18x+77=0,
(x-7)(x-11)=0,
解得x1=7,x2=11,
∵8≤x<12,
∴x=11.
答:能,x的值为11.
∴S=x(36-2x)=-2x2+36x.
|
解得8≤x<12
∴S=-2x2+36x(8≤x<12);
(2)-2x2+36x=154,
2x2-36x+154=0,
x2-18x+77=0,
(x-7)(x-11)=0,
解得x1=7,x2=11,
∵8≤x<12,
∴x=11.
答:能,x的值为11.
点评:考查二次函数的应用;得到矩形的另一边长是解决本题的易错点;注意应根据另一边长的局限得到相应的自变量的取值范围.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
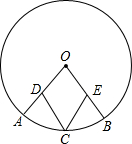 (2012•松北区一模)如图,在⊙0中,D、E分别为半径OA、OB上的点,且AD=BE.点C为弧AB中点,连接CD、CE.求证:CD=CE.
(2012•松北区一模)如图,在⊙0中,D、E分别为半径OA、OB上的点,且AD=BE.点C为弧AB中点,连接CD、CE.求证:CD=CE.