题目内容
阅读下面的材料:
∵ax2+bx+c=0(a≠0)的根为x1=
,x2=
.
∴x1+x2=
=-
,x1•x2=
=
.
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
,x1x2=
.
请利用这一结论解决问题
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)设方程2x2+3x+1=0的根为x1、x2,求
+
的值.
∵ax2+bx+c=0(a≠0)的根为x1=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
∴x1+x2=
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| c |
| a |
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
| b |
| a |
| c |
| a |
请利用这一结论解决问题
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)设方程2x2+3x+1=0的根为x1、x2,求
| 1 |
| x1 |
| 1 |
| x2 |
考点:根与系数的关系
专题:计算题
分析:(1)根据根与系数的关系得1+3=-b,1×3=c,然后计算即可;
(2)根据根与系数的关系得x1+x2=-
,x1•x2=
,再通分得
+
=
,然后利用整体思想计算即可.
(2)根据根与系数的关系得x1+x2=-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
解答:解:(1)根据题意得1+3=-b,1×3=c,
所以b=-4,c=3;
(2)根据题意得x1+x2=-
,x1•x2=
,
所以
+
=
=
=-3.
所以b=-4,c=3;
(2)根据题意得x1+x2=-
| 3 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
-
| ||
|
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 某大型生活超市销售一种进口奶粉A,从去年1至7月,这种奶粉的进价一路攀升,每罐A奶粉的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表:
某大型生活超市销售一种进口奶粉A,从去年1至7月,这种奶粉的进价一路攀升,每罐A奶粉的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表: 如图,在平面直角坐标系中,A(-3,-1),B(-3,-3),C(-2,-3),先把△ABC向右平移4个单位,得到△A1B1C1.
如图,在平面直角坐标系中,A(-3,-1),B(-3,-3),C(-2,-3),先把△ABC向右平移4个单位,得到△A1B1C1. 如图是某户人家全年各项支出的条形统计图,从图中可知这户人家的教育支出占全年总开支的百分数是
如图是某户人家全年各项支出的条形统计图,从图中可知这户人家的教育支出占全年总开支的百分数是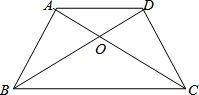 如图,四边形ABCD的对角线AC、BD相交于点O,OA=OD,OB=OC,则图中全等的三角形共有
如图,四边形ABCD的对角线AC、BD相交于点O,OA=OD,OB=OC,则图中全等的三角形共有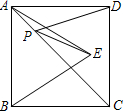 如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为
如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为