题目内容
 (2013•石景山区一模)已知:一次函数y=x+3与反比例函数y=
(2013•石景山区一模)已知:一次函数y=x+3与反比例函数y=| m-3 |
| x |
(1)求m的值和B点坐标;
(2)过A点作y轴的平行线,过B点作x轴的平行线,这两条直线交于点E,若反比例函数y=
| m-1 |
| x |
分析:(1)把A(a,2)先代入y=x+3求出a的值,则可确定A点坐标为(-1,2),再把A点坐标代入反比例函数解析式可计算出m的值,然后解由两解析式所组成的方程组即可得到B点坐标;
(2)先确定E点坐标(-1,1)和线段AB的中点坐标(-
,
),当反比例函数y=
的图象过E点时k最小,当反比例函数y=
的图象过线段AB的中点时k最大.
(2)先确定E点坐标(-1,1)和线段AB的中点坐标(-
| 3 |
| 2 |
| 3 |
| 2 |
| k |
| x |
| k |
| x |
解答:解:(1)∵一次函数y=x+3与反比例函数y=
(x<0)(m为常数)的图象交于点A(a,2)、B两点
∴
,解得
,
∴反比例函数的解析式为y=-
(x<0),
解方程组
得
,
,
∵A点坐标为(-1,2),
∴B点坐标为(-2,1);
(2)-
≤k≤-1.
| m-3 |
| x |

∴
|
|
∴反比例函数的解析式为y=-
| 2 |
| x |
解方程组
|
|
|
∵A点坐标为(-1,2),
∴B点坐标为(-2,1);
(2)-
| 9 |
| 4 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
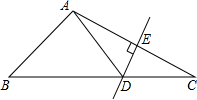 (2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
(2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) (2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
(2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )