题目内容
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

证明见解析.
【解析】
试题分析:(1)一方面Rt△ABC中,由∠BAC=30°可以得到AB=2BC,另一方面△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,从而可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF.
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
试题解析:证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
∵在Rt△AFE和Rt△BCA中,AF=BC,AE=BA,
∴△AFE≌△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.
∴四边形ADFE是平行四边形.
考点:1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的判定.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 ,则代数式
,则代数式 的值是 .
的值是 .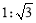 ,堤高BC=10m,则坡面AB的长度是( )
,堤高BC=10m,则坡面AB的长度是( )
 C.20m D.
C.20m D.
 ,则∠C的度数是( )
,则∠C的度数是( ) 分解因式,结果正确的是( )
分解因式,结果正确的是( ) B、
B、
 D、
D、
 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙