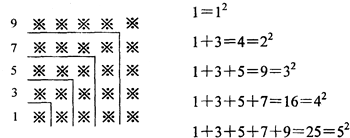题目内容
探索规律：
观察以下图形，并填写下表：
| 直线条数 | 1 | 2 | 3 | 4 | 5 | 6 | … | n |
| 最多交点个数 | 0 | 1 | 3 | 6 | … |
解：由题干规律可知，
n条直线相交比n-1条直线相交多n-1个交点，
故n条直线相交交点个数为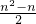
=
，
当n=5时，交点个数为10，
当n=6时，交点个数为15，
故答案为10，15，．
分析：两条直线相交有1个交点，二条直线相交由1个交点，三条直线相交有4个交点，四条直线相交有6个交点，可知在n条直线相交比n-1条直线相交多n-1个交点，故知n条直线的交点个数，即可推出5条直线，6条直线相交时交点的个数．
点评：本题主要考查直线、线段、射线的知识点，还涉及两直线交点问题，关键在于根据交点个数的变化总结出规律．
n条直线相交比n-1条直线相交多n-1个交点，
故n条直线相交交点个数为
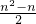=，当n=5时，交点个数为10，
当n=6时，交点个数为15，
故答案为10，15，
．分析：两条直线相交有1个交点，二条直线相交由1个交点，三条直线相交有4个交点，四条直线相交有6个交点，可知在n条直线相交比n-1条直线相交多n-1个交点，故知n条直线的交点个数，即可推出5条直线，6条直线相交时交点的个数．
点评：本题主要考查直线、线段、射线的知识点，还涉及两直线交点问题，关键在于根据交点个数的变化总结出规律．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
探索规律：
观察以下图形，并填写下表：
观察以下图形，并填写下表：
| 直线条数 | 1 | 2 | 3 | 4 | 5 | 6 | … | n |
| 最多交点个数 | 0 | 1 | 3 | 6 | … |
探索规律：观察下面由※组成的图案和算式，解答问题：