Question

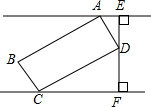（2012•湘潭）如图，矩形ABCD是供一辆机动车停放的车位示意图，已知BC=2m，CD=5.4m，∠DCF=30°，请你计算车位所占的宽度EF约为多少米？（

3

≈1.73，结果保留两位有效数字．）

Answer 1

分析：分别在直角三角形BCF和直角三角形AEF中求得DF和DE的长后相加即可得到EF的长．

解答：解：在直角三角形DCF中，
∵CD=5.4m，∠DCF=30°，
∴sin∠DCF=

FD

DC

=

DF

5.4

=

1

2

，
∴DF=2.7，
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°，
∴∠ADE=∠DCF，
∵AD=BC=2，
∴cos∠ADE=

DE

AD

=

ED

2

=

3

2

，
∴DE=

3

，
∴EF=ED+DF=2.7+1.732≈4.4米．

点评：本题考查了解直角三角形的应用，如何从纷杂的实际问题中整理出直角三角形是解决此类题目的关键．