题目内容
如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点恰好为BC边的中点D,过点D作⊙O的切线交AC于点E,
(1) 求证:DE⊥AC;
(2) 若AB=3DE,求tan∠ACB的值;

(1)(略)
(2)
设DE=b,EC=a,则AB=3b,AE=3b-a,∵AD⊥BC,DE⊥AC,易证∠C=∠ADE,
则△ADE∽△DCE,∴DE2=AE●EC,即: ,化简得:
,化简得: ;
;
解得: ,则
,则 ,故tan∠ACB=
,故tan∠ACB= ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
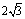 cm (C)4cm (D)
cm (C)4cm (D)  cm
cm
 (3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为( , ).
(3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为( , ). 的顶点坐标为 ;
的顶点坐标为 ;
 有意义的x的取值范围是 .
有意义的x的取值范围是 .