题目内容
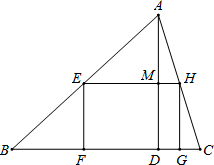 已知:如图:AD⊥BC于D,点E是边AB上一动点,四边形EFGH是矩形,其中点F,G在BC上,点H在AC上.
已知:如图:AD⊥BC于D,点E是边AB上一动点,四边形EFGH是矩形,其中点F,G在BC上,点H在AC上.
(1)若AD=BC,试探讨矩形EFGH的周长与高AD的数量关系;
(2)若矩形EFGH的面积是△ABC的面积的一半,求AE与AB的比值.
解(1)矩形EFGH的周长=2AD.理由如下:
∵四边形ABCD是矩形,
∴EH∥BC,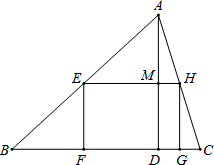
∴△AEH∽△ABC,
∵AD⊥BC于D,
∴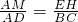 ,
,
设AM=x,则DM=AD-x,
∴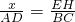 ,
,
∵AD=BC,
∴EH=x,
∵EF=DM=AD-x,
∴矩形EFGH的周长=2(EH+EF)=2(x+AD-x)=2AD,
∴矩形EFGH的周长=2AD;
(2)∵S△ABC= BC•AD,S矩形EFGH=EH•EF=EH•DM,
BC•AD,S矩形EFGH=EH•EF=EH•DM,
若矩形EFGH的面积是△ABC的面积的一半,
即 BC•AD=2EH•DM,
BC•AD=2EH•DM,
∴BC•AD=4EH•DM,
∵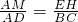 ,DM=AD-AM
,DM=AD-AM
∴EH=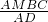 ,
,
∴BC•AD=4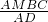 •(AD-AM),
•(AD-AM),
即AD2=4AM•AD-4AM2,
∴(AD-2AM)2=0,
∴AD=2AM,
∵EH∥BC,
∴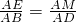 =
= .
.
分析:(1)由矩形的性质可得:EH∥BC,所以△AEH∽△ABC,利用相似三角形的性质:对应高之比等于相似比即可得到矩形EFGH的周长与高AD的数量关系;
(2)根据矩形的面积公式和三角形的面积公式分别把矩形EFGH的面积和△ABC的面积,利用图形中的线段表示出来,由(1)可知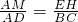 ,所以EH=
,所以EH=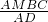 ,代入BC•AD=4EH•DM,进一步整理得到关于AD和2AM的完全平方公式,问题得解.
,代入BC•AD=4EH•DM,进一步整理得到关于AD和2AM的完全平方公式,问题得解.
点评:此题主要考查了相似三角形的判定与性质、矩形的性质以及矩形的面积和三角形的面积公式的运用,题目的设计很新颖,特别是第二问根据条件得到比例式,再进一步整理得到完全平方公式是解题的突破口.
∵四边形ABCD是矩形,
∴EH∥BC,

∴△AEH∽△ABC,
∵AD⊥BC于D,
∴
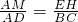 ,
,设AM=x,则DM=AD-x,
∴
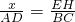 ,
,∵AD=BC,
∴EH=x,
∵EF=DM=AD-x,
∴矩形EFGH的周长=2(EH+EF)=2(x+AD-x)=2AD,
∴矩形EFGH的周长=2AD;
(2)∵S△ABC=
 BC•AD,S矩形EFGH=EH•EF=EH•DM,
BC•AD,S矩形EFGH=EH•EF=EH•DM,若矩形EFGH的面积是△ABC的面积的一半,
即
 BC•AD=2EH•DM,
BC•AD=2EH•DM,∴BC•AD=4EH•DM,
∵
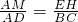 ,DM=AD-AM
,DM=AD-AM∴EH=
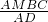 ,
,∴BC•AD=4
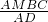 •(AD-AM),
•(AD-AM),即AD2=4AM•AD-4AM2,
∴(AD-2AM)2=0,
∴AD=2AM,
∵EH∥BC,
∴
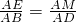 =
= .
.分析:(1)由矩形的性质可得:EH∥BC,所以△AEH∽△ABC,利用相似三角形的性质:对应高之比等于相似比即可得到矩形EFGH的周长与高AD的数量关系;
(2)根据矩形的面积公式和三角形的面积公式分别把矩形EFGH的面积和△ABC的面积,利用图形中的线段表示出来,由(1)可知
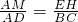 ,所以EH=
,所以EH=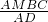 ,代入BC•AD=4EH•DM,进一步整理得到关于AD和2AM的完全平方公式,问题得解.
,代入BC•AD=4EH•DM,进一步整理得到关于AD和2AM的完全平方公式,问题得解.点评:此题主要考查了相似三角形的判定与性质、矩形的性质以及矩形的面积和三角形的面积公式的运用,题目的设计很新颖,特别是第二问根据条件得到比例式,再进一步整理得到完全平方公式是解题的突破口.

练习册系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.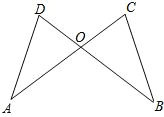 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.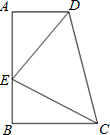 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC. 根据题意填空:
根据题意填空: