题目内容
 如图,∠ACB=90゜,CA=CB,D为BC上一点,BM⊥AD于M,CN⊥AD于N.求证:BM+CN=AN.
如图,∠ACB=90゜,CA=CB,D为BC上一点,BM⊥AD于M,CN⊥AD于N.求证:BM+CN=AN.分析:首先根据已知得出∠ACN=∠BCE,进而证明△ACN≌△BCE(AAS),得出AN=BE,再得出四边形CNME是矩形,即可得出答案.
解答: 证明:过C作CE⊥BM于E,
证明:过C作CE⊥BM于E,
由题意可得出:∠CND=∠BMD,∠CDN=∠BDM,
∴∠NCD=∠MBD,
∵∠MBD+∠ECB=90°,∠ACN+∠BCN=90°,
∴∠ACN=∠BCE,
在△ACN和△BCE中
,
∴△ACN≌△BCE(AAS),
∴AN=BE,
∵∠CNM=∠AME=∠E=90°,
∴四边形CNME是矩形,
∴CN=EM,
∴BM+CN=BE=AN.
 证明:过C作CE⊥BM于E,
证明:过C作CE⊥BM于E,由题意可得出:∠CND=∠BMD,∠CDN=∠BDM,
∴∠NCD=∠MBD,
∵∠MBD+∠ECB=90°,∠ACN+∠BCN=90°,
∴∠ACN=∠BCE,
在△ACN和△BCE中
|
∴△ACN≌△BCE(AAS),
∴AN=BE,
∵∠CNM=∠AME=∠E=90°,
∴四边形CNME是矩形,
∴CN=EM,
∴BM+CN=BE=AN.
点评:此题主要考查了全等三角形的判定与性质,本题实质是间接地将CN补在BM后面的EM处是解题关键.

练习册系列答案
相关题目
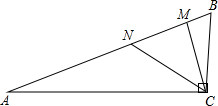 如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是
如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是 10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( )
10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( ) 如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( ) 如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE.
如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE. 如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.
如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.