Question

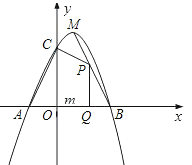
【题目】如图，在平面直角坐标系中，抛物线交轴于，两点，与轴交于点.连接.

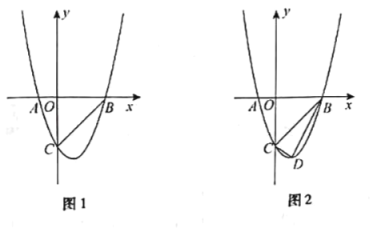
（1）求抛物线的解析式和点的坐标；

（2）“若点为第四象限内抛物线上一动点，点的横坐标为，的面积为，求关于的函数关系式，并求出的最大值；

（3）抛物线的对称轴上是否存在点，使为等腰三角形？若存在，请直接写出所有点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）当时，的最大值为；（3）抛物线的对称轴上存在点，使为等腰三角形，点的坐标为，，,或

【解析】

（1）把，代入得到关于b,c的二元一次方程组，解方程组即可求出抛物线的解析式，再令x=0，即可求出y的值，从而得到C的坐标；

（2）连接OD，则，分别用含x的式子表示出这三个三角形的面积，从而得到s与x的函数关系式；

（3）分情况进行讨论即可.

解：（1）把，代入，得

，解得

∴抛物线的解析式为

当时，

∴

（2）∵点的横坐标为，在抛物线上

∴点的纵坐标为

∴

∵点在第四象限

∴，

如图，连接

∵

∵，

∴当时，的最大值为

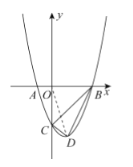
（3）抛物线的对称轴上存在点，使为等腰三角形，点的坐标为，，,或.理由如下：

∵B(3,0),C(0,-3),

∴BC=3 ,

∵抛物线的对称轴是x=1,

∴OD=1,BD=OB-OD=2.

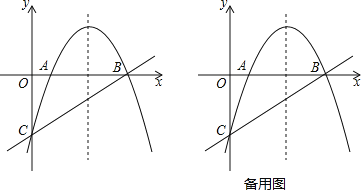
①当BP=BC时，如图1，

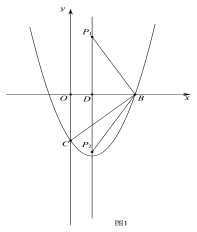
∵抛物线的对称轴是x=1,

∴OD=1,BD=OB-OD=2.

在Rt△BPD中，

PD=

=

=

∴此时点P的坐标为或.

② 当CP=BC=3 时，如图2，

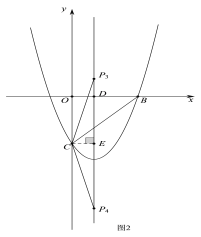
在Rt△CPE中，PE==

∴此时点P的坐标为，.

③当CP=BP时，如图3，

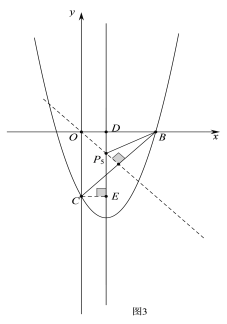
∵OB=OC,OP⊥BC，

∴∠BOP=45°，

∵∠ODP=90°，

∴∠DOP=∠OPD=45°，

∴PD=OD=1,

∴此时点P的坐标为，

综上所述，抛物线的对称轴上存在点，使为等腰三角形，点的坐标为，，,或.