题目内容
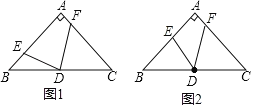
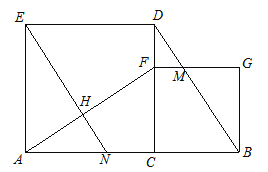
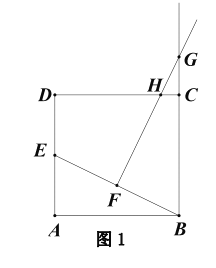
【题目】如图1,矩形ABCD中,AD=2,AB=a,点E为AD的中点,连接BE.过BE的中点F作FG⊥BE,交射线BC于点G,交边CD于H点.
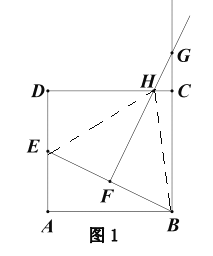
(1)连接HE、HB
①求证:HE=HB;
②若a=4,求CH的长.
(2)连接EG,△BEG面积为S
①BE= (用含a的代数式表示);
②求S与a的函数关系式.
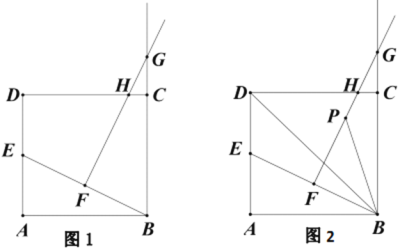
(3)如图2,设FG的中点为P,连接PB、BD.猜想∠GBP与∠DBE的关系,并说明理由.
【答案】(1)①详见解析;②![]() ;(2)①BE=
;(2)①BE=![]() ;②
;②![]() ;(3)猜想:∠GBP=∠DBE;详见解析
;(3)猜想:∠GBP=∠DBE;详见解析
【解析】
(1)①证明![]() 是
是![]() 的垂直平分线,即可得到答案,②先求解
的垂直平分线,即可得到答案,②先求解![]() ,利用
,利用![]() 由三角函数建立联系,求解
由三角函数建立联系,求解![]() 再求解
再求解![]() 由同角的三角函数求解
由同角的三角函数求解![]() 即可,
即可,
(2)①利用勾股定理直接得到答案,②先求解![]() ,利用
,利用![]() 由三角函数建立联系,求解
由三角函数建立联系,求解![]() 从而可得答案,
从而可得答案,
(3)过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() ,证明
,证明![]() 即可得到答案.
即可得到答案.
证明:(1)①如图,![]()
![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
②![]() 为
为![]() 的中点,
的中点,![]()
![]()
![]() 矩形
矩形![]()
![]()
![]()
![]()
![]() 为
为![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
![]()
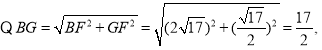
![]()
![]()
![]()
![]()
(2)①由![]()
![]()
故答案为:![]()
②![]() 为
为![]() 的中点,
的中点,
![]()
由①知:
![]()
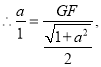
![]()
![]()
![]()
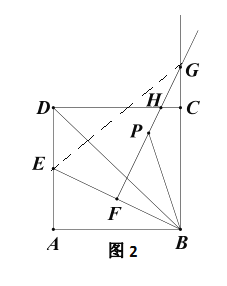
(3)![]() ,理由如下:
,理由如下:
证明:过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() ,
,
则![]()
![]()
![]()
![]()
![]()
![]()
![]()
由![]()
![]()
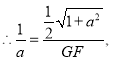
![]()
![]() 为
为![]() 的中点,
的中点,
![]()
![]()
![]()
由![]()
![]()
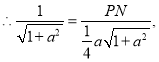
![]()
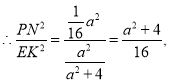
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目