题目内容
（2003•泰安）关于x的不等式组
有四个整数解，则a的取值范围是（ ）A．-
＜a≤-
B．-
≤a＜-
C．-
≤a≤-
D．-
＜a＜-
【答案】分析：先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求a的取值范围即可．
解答：解：由（1）得x＞8；
由（2）得x＜2-4a；
其解集为8＜x＜2-4a，
因不等式组有四个整数解，为9，10，11，12，则
，
解得-
≤a＜-
．
故选B．
点评：考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
解答：解：由（1）得x＞8；
由（2）得x＜2-4a；
其解集为8＜x＜2-4a，
因不等式组有四个整数解，为9，10，11，12，则
，解得-
≤a＜-．故选B．
点评：考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
有四个整数解，则a的取值范围是（ ）
＜a≤-
≤a＜-
≤a≤-
＜a＜-
（2003•泰安）（1）用计算器探索：
①
=
②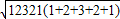
=
③
=
由此猜想：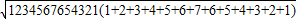
=______．
（2）已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1、x2满足x12+x22=2，则a的值为______．
①
=②
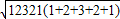=③
=由此猜想：
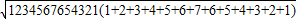=______．（2）已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1、x2满足x12+x22=2，则a的值为______．
=
=
=
=______．
=
=
=
=______．