题目内容
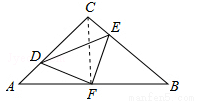
(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中
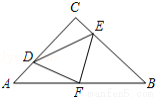
(1)求证:△DFE是等腰直角三角形.
(2)求DE长度的最小值.
(3)求△CDE面积的最大值.
(1)证明见试题解析;(2)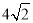 ;(3)8.
;(3)8.
【解析】
试题分析:(1)连接CF,由SAS定理可得△CFE≌△ADF,从而可证∠DFE=90°可得DF=EF,可得△DFE是等腰直角三角形;
(2)由DE=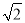 DF,当DF最小时,DE也最小,而当DF⊥AC时,DF最小,DE取最小值
DF,当DF最小时,DE也最小,而当DF⊥AC时,DF最小,DE取最小值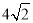 ;
;
(3)由△ADF≌△CEF,得到S△CEF=S△ADF,故S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=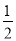 S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
试题解析:(1)连接CF,∵△ABC为等腰直角三角形,∴∠FCB=∠A=45°,CF=AF=FB,∵AD=CE,∴△ADF≌△CEF,∴EF=DF,∠CFE=∠AFD,∵∠AFD+∠CFD=90°,∴∠CFE+∠CFD=∠EFD=90°,∴△EDF是等腰直角三角形;
(2)∵△DEF是等腰直角三角形,∴当DE最小时,DF也最小,即当DF⊥AC时,DE最小,此时DF=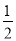 BC=4,∴DE=
BC=4,∴DE=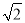 DF=
DF=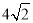 ;
;
(3)∵△ADF≌△CEF,∴S△CEF=S△ADF,∴S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=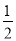 S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
考点:1.等腰直角三角形;2.全等三角形的判定与性质.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

读取表格中的信息,解决问题.满足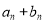 >1000的n可以取得的最小正整数是 .
>1000的n可以取得的最小正整数是 .
n=1 |
|
|
n=2 |
|
|
n=3 |
|
|
… | … | … |
 的倒数是( )
的倒数是( ) B.
B. C.
C. D.
D.





 .
.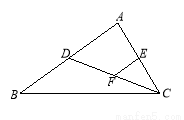
 ,再将x取一个喜欢的值代入计算.(6分)
,再将x取一个喜欢的值代入计算.(6分) 的值为零.
的值为零.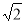 ,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
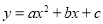 (
( )的图象如图所示,下列说法错误的是( )
)的图象如图所示,下列说法错误的是( )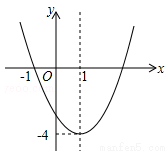
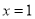 对称
对称 时,y随x的增大而减小
时,y随x的增大而减小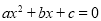 (
(