Question

迎迎拿来奥运场馆建设中的一张图纸，已知：在△ABC中，AD，AE分别是△ABC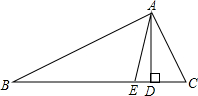的高和角平分线，若∠B=30°，∠C=50°．你能帮助工人师傅解决下面的问题吗？
（1）求∠DAE的度数．
（2）试写出∠DAE与∠C-∠B有何关系？（不必证明）

Answer 1

分析：（1）根据三角形内角和等于180°求出∠BAC的度数，然后根据AE是角平分线求出∠CAE的度数，在△ACD中，利用直角三角形两锐角互余求出∠CAD的度数，两角相减即可求解；
（2）同（1）的思路整理即可．

解答：解：（1）∵∠B=30°，∠C=50°，
∴∠BAC=180°-30°-50°=100°，
∵AE是△ABC的角平分线，
∴∠CAE=

1

2

∠BAC=

1

2

×100°=50°，
∵AD是△ABC的高，∠C=50°，
∴∠CAD=90°-50°=40°，
∴∠DAE=∠CAE-∠CAD=50°-40°=10°；

（2）同（1）的思路，∠CAE=

1

2

∠BAC=

1

2

（180°-∠B-∠C）=90°-

1

2

∠B-

1

2

C，
∠CAD=90°-∠C，
∴∠DAE=∠CAE-∠CAD=90°-

1

2

∠B-

1

2

C-（90°-∠C）=

1

2

（∠C-∠B）．

点评：本题考查了三角形的内角和定理，角平分线的定义，直角三角形两锐角互余的性质，结合图形找准思路便不难解决．