Question

如图，已知△ABC，按如下步骤作图：①分别以A、C为圆心，以大于的长为半径在AC两边作弧，交于两点M、N；②作直线MN，分别交AB、AC于点D、O；③过C作CE∥AB交MN于点E，连接AE、CD．

（1）求证：四边形ADCE是菱形；
（2）当∠ACB90°，BC6，AB10，求四边形ADCE的面积．

Answer 1

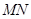（1）由题意得是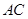的垂直平分线，根据垂直平分线的性质可得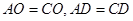，再根据平行线的性质可得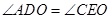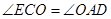，，即可证得△AOD≌△COE，从而可得四边形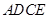是平行四边形，再结合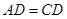即可证得结论；（2）24

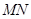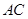解析试题分析：（1）由题意得是的垂直平分线，根据垂直平分线的性质可得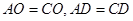，再根据平行线的性质可得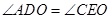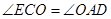，，即可证得△AOD≌△COE，从而可得四边形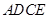是平行四边形，再结合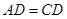即可证得结论；
（2）由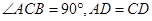可证得OD是△ABC的中位线，根据三角形的中位线定理及勾股定理再结合三角形的面积公式即可求得结果.
（1）由题意得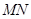是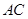的垂直平分线，
∴
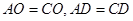
∵CE∥AB
∴，
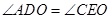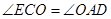
∴△AOD≌△COE
∴
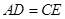
∴四边形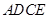是平行四边形
∵
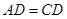
∴四边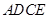形是菱形
（2）∵


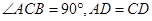
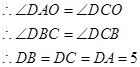
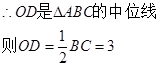
由勾股定理得AC=8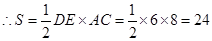
.
考点：垂直平分线的性质，平行线的性质，全等三角形的判定和性质，平行四边形的判定，菱形的判定，三角形的中位线定理，勾股定理，三角形的面积公式
点评：本题知识点多，综合性强，是中考常见题，一般难度不大，学生需熟练掌握平面图形的基本性质.