题目内容
如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.若 ,则BN的长是 ,
,则BN的长是 , 的值等于 ;若
的值等于 ;若 (n≥2,且n为整数),则
(n≥2,且n为整数),则 的值等于 (用含n的式子表示).
的值等于 (用含n的式子表示).
【答案】分析:求出CE,根据勾股定理求出BN、EN,证△DEQ∽△CNE,求出DQ、QE长,在Rt△MFQ中,根据勾股定理求出AM即可.
解答:解:∵沿MN折叠B和E重合,
∴BN=NE,
∵ =
= ,CD=2,
,CD=2,
∴CE=1,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=12+(2-x)2
x= ,
,
BN=NE= .
.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴ =
= =
= ,
,
∴ =
= =
= ,
,
DQ= ,EQ=
,EQ= ,
,
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2- -AM)2=AM2+(2-
-AM)2=AM2+(2- )2,
)2,
AM= .
.
∵沿MN折叠B和E重合,
∴BN=NE,
∵ =
= ,CD=2,
,CD=2,
∴CE= ,
,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=( )2+(2-x)2
)2+(2-x)2
x= ,
,
BN=NE= .
.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴ =
= =
= ,
,
∴ =
= =
= ,
,
DQ= ,EQ=
,EQ= ,
,
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2- -AM)2=AM2+(2-
-AM)2=AM2+(2- )2,
)2,
AM= ,
,
∴ =
= ,
,
故答案为: ,
, ,
, .
.
点评:本题考查了折叠的性质,正方形性质,相似三角形的性质和判定等知识点的应用,注意:折叠前后两图形全等,即对应线段相等,对应角相等,用了方程思想.
解答:解:∵沿MN折叠B和E重合,
∴BN=NE,
∵
 =
= ,CD=2,
,CD=2,∴CE=1,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=12+(2-x)2
x=
 ,
,BN=NE=
 .
.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
 =
= =
= ,
,∴
 =
= =
= ,
,DQ=
 ,EQ=
,EQ= ,
,∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
 -AM)2=AM2+(2-
-AM)2=AM2+(2- )2,
)2,AM=
 .
.∵沿MN折叠B和E重合,
∴BN=NE,
∵
 =
= ,CD=2,
,CD=2,∴CE=
 ,
,设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=(
 )2+(2-x)2
)2+(2-x)2x=
 ,
,BN=NE=
 .
.∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
 =
= =
= ,
,∴
 =
= =
= ,
,DQ=
 ,EQ=
,EQ= ,
,∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
 -AM)2=AM2+(2-
-AM)2=AM2+(2- )2,
)2,AM=
 ,
,∴
 =
= ,
,故答案为:
 ,
, ,
, .
.点评:本题考查了折叠的性质,正方形性质,相似三角形的性质和判定等知识点的应用,注意:折叠前后两图形全等,即对应线段相等,对应角相等,用了方程思想.

练习册系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
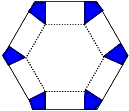 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为