Question

如图，已知抛物线y=ax²+c交x轴于点A（-1，0）和点B，交y轴于点C（0，-1）．
（1）求此抛物线的解析式．
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．

Answer 1

解：（1）∵抛物线y=ax²+c过A（-1，0）和C（0，-1）
∴，
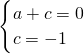解得：，
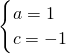∴抛物线解析式为：y=x²-1；

（2）令y=0，x²-1=0，
解得：x₁=1，x₂=-1
∴B（1，0），
∵A（-1，0），C（0，-1）
∴OA=OB=OC=1，
∴∠BAC=∠ACO=∠BCO=45°，
∵AP∥CB，
∴∠PAB=45°
过点P作PE⊥x轴于E，则△APE为等腰直角三角形
令OE=a，则PE=a+1，
∴P（a，a+1），
∵点P在抛物线y=x²-1上，
∴a+1=a²-1
解得a₁=2，a₂=-1（不符合题意）
∴PE=3
∴四边形ACBP的面积S=AB•OC+AB•PE
=×2×1+×2×3
=4．
分析：（1）利用待定系数法直接将点的坐标代入抛物线的解析式求出a、c的值就可以求出抛物线的解析式．
（2）利用抛物线的解析式，求出点A、B、C的坐标，求出△ABC的形状，利用平行线的性质求出∠PAB的度数，将四边形分为两个三角形的面积求和就可以了．
点评：此题主要考查了待定系数法求二次函数的解析式、平行线的性质相以及多边形的面积求法，利用等腰直角三角形的性质得出P点坐标是解题关键．