题目内容
【题目】如图,在□ABCD中,AB=10,BC=5,BN平分∠ABC交CD于点N,交AD的延长线于点M,则下列结论:①DM=5;②线段BM、CD互相平分;③BD⊥AM;④△BCN是等边三角形;⑤AN⊥BM,其中正确的有______________(填序号).

【答案】①②⑤
【解析】
①通过判断![]() ,即可得到
,即可得到![]() ;②通过判断
;②通过判断![]() ,即可得到
,即可得到![]() ,
,![]() ,即可得到线段BM、CD互相平分;③由于无法求证BA=BM从而无法得到BD⊥AM;④根据题意求证
,即可得到线段BM、CD互相平分;③由于无法求证BA=BM从而无法得到BD⊥AM;④根据题意求证![]() 是等腰三角形但不是等边三角形;⑤通过求证
是等腰三角形但不是等边三角形;⑤通过求证![]() 是等腰三角形,再根据三线合一即可得解.
是等腰三角形,再根据三线合一即可得解.
①∵四边形ABCD是平行四边形
∴![]() ,
,![]()
∴![]() ,
,![]()
∵BN平分∠ABC
∴![]()
∴![]()
∴![]()
∵BC=5,AB=10
∴![]()
在![]() 与
与![]() 中
中
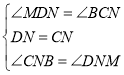
∴![]()
∴![]() ,故①正确;
,故①正确;
②∵![]()
∴![]()
又∵![]()
∴线段BM、CD互相平分,故②正确;
③∵由四边形ABCD是平行四边形得![]()
∴![]()
但是题中条件不足以证明![]() ,则无法根据三线合一求证BD⊥AM,故③错误;
,则无法根据三线合一求证BD⊥AM,故③错误;
④由①可知![]() ,但是无法证明
,但是无法证明![]() ,故④错误;
,故④错误;
⑤由③得![]() ,由②得
,由②得![]() ,则由三线合一可知AN⊥BM,故⑤正确,
,则由三线合一可知AN⊥BM,故⑤正确,
综上,正确的有①②⑤,
故答案为:①②⑤.

练习册系列答案
相关题目