题目内容
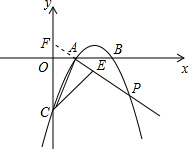
 如图,抛物线y=-x2+4x-3与坐标轴交于A、B、C三点,将△OAC沿AC翻折得到△ACE,直线AE交抛物线于P点,求直线AP的解析式和P点坐标.
如图,抛物线y=-x2+4x-3与坐标轴交于A、B、C三点,将△OAC沿AC翻折得到△ACE,直线AE交抛物线于P点,求直线AP的解析式和P点坐标.分析:点P为直线AE和抛物线的交点,欲求点P,必须先求出直线AE的解析式;设直线AE与y轴的交点为F,易得△FOA∽△FEC,由于OA=1,EC=3,根据相似三角形的对应边成比例即可得到FE=3OF,设OF=x,则EF=3x,AF=3x-1,进而可在Rt△FOA中求出x的值,也就能求出F点的坐标,然后利用待定系数法求出直线AE的解析式,联立抛物线的解析式即可得到点P的坐标.
解答:解:∵y=-x2+4x-3=-(x-1)(x-3),
∴A(1,0),B(3,0).
令x=0,则y=-3,则C(0,-3).
如图, 设AE交y轴于点F;
设AE交y轴于点F;
易证得△FOA∽△FEC,有
=
=
,
设OF=x,则EF=3x,
所以FA=3x-1;
在Rt△FOA中,由勾股定理得:
(3x-1)2=x2+1,
解得x=
;
即OF=
,F(0,
);
求得直线AE为y=-
x+
,联立抛物线的解析式得:
,
解得
或
(不合题意,舍去).
故点P(
,-
).
∴A(1,0),B(3,0).
令x=0,则y=-3,则C(0,-3).
如图,
 设AE交y轴于点F;
设AE交y轴于点F;易证得△FOA∽△FEC,有
| FO |
| FE |
| OA |
| CE |
| 1 |
| 3 |

设OF=x,则EF=3x,
所以FA=3x-1;
在Rt△FOA中,由勾股定理得:
(3x-1)2=x2+1,
解得x=
| 3 |
| 4 |
即OF=
| 3 |
| 4 |
| 3 |
| 4 |
求得直线AE为y=-
| 3 |
| 4 |
| 3 |
| 4 |
|
解得
|
|
故点P(
| 15 |
| 4 |
| 33 |
| 16 |
点评:此题考查了二次函数解析式的确定、函数图象交点坐标的求法、图形的旋转变化、全等三角形的判定和性质以及函数图象上点的坐标意义等知识.

练习册系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.