题目内容
 (2012•河北)如图,在平行四边形ABCD中,∠A=70°,将平行四边形折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
(2012•河北)如图,在平行四边形ABCD中,∠A=70°,将平行四边形折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )分析:由平行四边形与折叠的性质,易得CD∥MN∥AB,然后根据平行线的性质,即可求得∠DMN=∠FMN=∠A=70°,又由平角的定义,即可求得∠AMF的度数.
解答:解:∵四边形ABCD是平行四边形,
∴AB∥CD,
根据折叠的性质可得:MN∥AE,∠FMN=∠DMN,
∴AB∥CD∥MN,
∵∠A=70°,
∴∠FMN=∠DMN=∠A=70°,
∴∠AMF=180°-∠DMN-∠FMN=180°-70°-70°=40°.
故选B.
∴AB∥CD,
根据折叠的性质可得:MN∥AE,∠FMN=∠DMN,
∴AB∥CD∥MN,
∵∠A=70°,
∴∠FMN=∠DMN=∠A=70°,
∴∠AMF=180°-∠DMN-∠FMN=180°-70°-70°=40°.
故选B.
点评:此题考查了平行四边形的性质、平行线的性质与折叠的性质.此题难度不大,注意数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
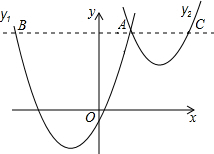 (2012•河北)如图,抛物线y1=a(x+2)2-3与y2=
(2012•河北)如图,抛物线y1=a(x+2)2-3与y2= (2012•河北)如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( )
(2012•河北)如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( ) (2012•河北)如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a-b)等于( )
(2012•河北)如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a-b)等于( ) (2012•河北)如图,AB、CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A=
(2012•河北)如图,AB、CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A=