题目内容
【题目】如图,已知⊙O的半径为2,弦AB⊥半径OC,沿AB将弓形ACB翻折,使点C与圆心O重合,则月牙形(图中实线围成的部分)的面积是 . 
【答案】![]() π+2
π+2 ![]()
【解析】解:连接OA,OB, 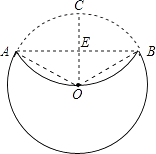
∵OC⊥AB于E,
根据题意,得OE= ![]() OC=
OC= ![]() OB=1,
OB=1,
则∠ABO=30°,BE= ![]() =
= ![]() ,
,
∴AB=2 ![]() ,∠AOB=120°.
,∠AOB=120°.
S弓形ACB=S扇形AOB﹣S△AOB= ![]() ﹣
﹣ ![]() AB×EO=
AB×EO= ![]() π﹣
π﹣ ![]() ,
,
则月牙形(图中实线围成的部分)的面积是:S圆﹣2S弓形ACB=4π﹣2( ![]() π﹣
π﹣ ![]() )=
)= ![]() π+2
π+2 ![]() ,
,
所以答案是: ![]() π+2
π+2 ![]() .
.
【考点精析】根据题目的已知条件,利用扇形面积计算公式和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】为激励教师爱岗敬业,某市开展了“我最喜爱的老师”评选活动.某中学确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整). 学生投票结果统计表
候选教师 | 王老师 | 赵老师 | 李老师 | 陈老师 |
得票数 | 200 | 300 |

(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)王老师与李老师得到的学生总票数是500,且王老师得到的学生票数是李老师得到的学生票数的3倍多20票,求王老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?





