Question

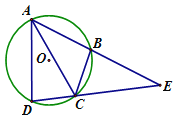
【题目】如图，AB是⊙O的弦，AC与⊙O相切于点A，且∠BAC=52°．

（1）求∠OBA的度数；

（2）求∠D的度数．

Answer 1

【答案】（1）38°；（2）52°．

【解析】

（1）连接OA，由切线的性质可得∠OAC=90°，再由已知条件可求出∠OAB的度数，由圆的性质可得△OAB是等腰三角形，根据等边对等角即可求出∠OBA的度数；

（2）由（1）可知△OAB是等腰三角形，所以∠AOB的度数可求，再由圆周角定理即可求出∠D度数．

（1）连接OA，

∵AC与⊙O相切于点A，

∴OA⊥AC，

∴∠OAC=90°，

∵∠BAC=52°，

∴∠OAB=38°，

∵OA=OB，

∴∠OBA=∠OAB=38°；

（2）∵∠OBA=∠OAB=38°，

∴∠AOB=180°﹣2×38°=104°，

∴∠D=∠AOB=52°．