Question

【题目】观察表格：根据表格解答下列问题：

x	0	1	2
ax2	0	1	4
ax2+bx+c	﹣3	-4	﹣3

（l）求a，b，c的值；

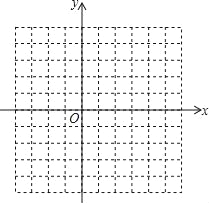
（2）在如图的直角坐标系中画出函数y=ax2+bx+c的图象，并根据图象，直接写出当x取什么实数时，不等式ax2+bx+c＞﹣3成立；

（3）该图象与x轴两交点从左到右依次分别为A、B，与y轴交点为C，求过这三个点的外接圆的半径．

Answer 1

【答案】（1）1，﹣2，﹣3；（2）当x＜0或x＞2时，不等式ax2+bx+c＞﹣3成立；

（3）△ABC的外接圆的半径r=O′B=.

【解析】

（1）利用待定系数法即可解决问题；

（2）利用描点法画出函数图象，根据图象写出函数值大于﹣3得到自变量x的取值范围即

可；

（3）想办法求出△ABC的外接圆的圆心坐标即可；

（1）由题意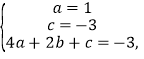 解得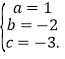

（2）函数图象如图所示：当x＜0或x＞2时，不等式ax2+bx+c＞﹣3成立；

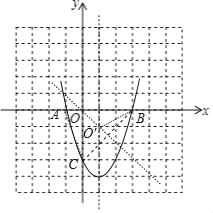
（3）由题意A（﹣1，0），B（3，0），C（0，3），

∴OB=OC=3，

∴△ABC的外接圆的圆心O′是直线y=﹣x与直线x=1的交点，

∴O′（1，﹣1），

∴△ABC的外接圆的半径