Question

【题目】如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为 ．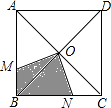

Answer 1

【答案】
【解析】解：∵四边形ABCD为正方形，点O是对角线的交点， ∴∠MBO=∠NCO=45°，OB=OC，∠BOC=90°，
∵∠MON=90°，
∴∠MOB+∠BON=90°，∠BON+∠NOC=90°，
∴∠MOB=∠NOC．
在△MOB和△NOC中，有 ，
∴△MOB≌△NOC（ASA）．
同理可得：△AOM≌△BON．
∴S阴影=S△BOC= S正方形ABCD ．
∴蚂蚁停留在阴影区域的概率P= = ．
故答案为： ．
根据正方形的性质可得出“∠MBO=∠NCO=45°，OB=OC，∠BOC=90”，通过角的计算可得出∠MOB=∠NOC，由此即可证出△MOB≌△NOC，同理可得出△AOM≌△BON，从而可得知S阴影= S正方形ABCD ， 再根据几何概率的计算方法即可得出结论．