Question

【题目】已知：如图，△ABC，△ADE均为等腰直角三角形，点D，E，C在同直线上，连接BD．

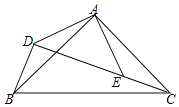
（1）求证：△ADB≌△AEC；（2）求∠BDC的度数．

Answer 1

【答案】（1）见解析；（2）∠BDC=90°

【解析】

(1)通过已知条件求出AD=AE，∠DAB=∠EAC，AB=AC，通过SAS即可证明△ADB≌△AEC；

(2)通过(1)中的全等，可得∠ADB=∠AEC，通过直角三角形∠ADE=∠AED=45°，∠BDC=∠AEC-∠ADE即可求得．

(1)∵△ABC，△ADE均为等腰直角三角形，

∴AD=AE，AB=AC，∠DAE=∠BAC=90°，

∵∠DAB=∠DAE-∠BAE=90°-∠BAE，∠EAC=∠BAC-∠BAE=90°-∠BAE，

∴∠DAB=∠EAC，

在△ADB和△AEC中，

，

∴△ADB≌△AEC(SAS)；

(2)由(1)得：△ADB≌△AEC，∴∠ADB=∠AEC，

∵△ADE均为等腰直角三角形，

∴∠ADE=∠AED=45°，

∴∠AEC=180°-∠ADE=180°-45°=135°，

∴∠AEC=∠ADB=135°，

∴∠BDC=∠AEC-∠ADE=135°-45°=90°