题目内容
【题目】在半径为25cm的⊙O中，弦AB＝40cm，则弦AB所对的弧的中点到AB的距离是（ ）
A.10cmB.15cmC.40cmD.10cm或40cm
【答案】D
【解析】
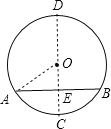
点C和D为弦AB所对弧的中点，连结CD交AB于E，连结OA，如图，根据垂径定理的推论得到CD为直径，CD⊥AB，则AE＝BE＝
AB＝20，再利用勾股定理计算出OE＝15，然后分别计算出DE和CE即可．
解：点C和D为弦AB所对弧的中点，连结CD交AB于E，连结OA，如图，
∵点C和D为弦AB所对弧的中点，
∴CD为直径，CD⊥AB，
∴AE＝BE＝AB＝20，
在Rt△OAE中，∵OA＝25，AE＝20，
∴OE＝
，
∴DE＝OD+OE＝40，CE＝OC﹣OE＝10，
即弦AB和弦AB所对的劣弧的中点的距离为10cm，弦AB和弦AB所对的优弧的中点的距离为40cm．
故选：D．
练习册系列答案
相关题目
