题目内容
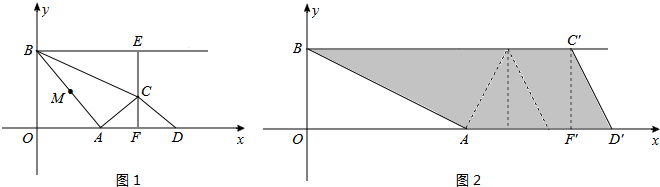
（2013•丽水）如图1，在Rt△ABC中，∠ACB=90°，点P以每秒1cm的速度从点A出发，沿折线AC-CB运动，到点B停止，过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示，当点P运动5秒时，PD的长是（ ）分析：根据图2可判断AC=3，BC=4，则可确定t=5时BP的值，利用sin∠B的值，可求出PD．
解答：解：由图2可得，AC=3，BC=4，
当t=5时，如图所示：
，
此时AC+CP=5，故BP=AC+BC-AC-CP=2，
∵sin∠B=
=
，
∴PD=BPsin∠B=2×
=
=1.2cm．
故选B．
当t=5时，如图所示：
，此时AC+CP=5，故BP=AC+BC-AC-CP=2，
∵sin∠B=
| AC |
| AB |
| 3 |
| 5 |
∴PD=BPsin∠B=2×
| 3 |
| 5 |
| 6 |
| 5 |
故选B．
点评：本题考查了动点问题的函数图象，解答本题的关键是根据图2得到AC、BC的长度，此题难度一般．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
（2013•丽水）如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是
（2013•丽水）如图，AB∥CD，AD和BC相交于点O，∠A=20°，∠COD=100°，则∠C的度数是（ ）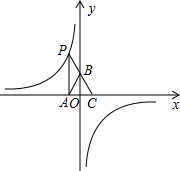
（2013•丽水）如图，点P是反比例函数y=
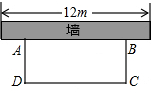（2013•丽水）如图，科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD，其中一边AB靠墙，墙长为12 m．设AD的长为x m，DC的长为y m．