题目内容
阅读材料：设一元二次方程ax2+bx+c=0的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．根据该材料填空：已知x1，x2是方程x2+5x-4=0的两实数根，则
+
+2的值为
| b |
| a |
| c |
| a |
| x2 |
| x1 |
| x1 |
| x2 |
-
| 25 |
| 4 |
-
．| 25 |
| 4 |
分析：根据一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系得到x1+x2=-5，x1•x2=-4，再变形
+
+2得
+2=
，然后把x1+x2=-5，x1•x2=-4整体代入计算即可．
| x2 |
| x1 |
| x1 |
| x2 |
| x12+x22 |
| x1x2 |
| (x1+x2)2 |
| x1x2 |
解答：解：根据题意得x1+x2=-5，x1•x2=-4，
+
+2
=
+2
=
=
=-
．
故答案为-
．
| x2 |
| x1 |
| x1 |
| x2 |
=
| x12+x22 |
| x1x2 |
=
| (x1+x2)2 |
| x1x2 |
=
| (-5)2 |
| -4 |
=-
| 25 |
| 4 |
故答案为-
| 25 |
| 4 |
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两根分别为x1，x2，则x1+x2=-
，x1•x2=
．也考查了代数式的变形能力．
| b |
| a |
| c |
| a |
练习册系列答案
快捷英语周周练系列答案
相关题目
20、阅读材料，解答问题．
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
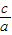根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，当0＜x1＜1，2＜x2＜3时，试判断y1与y2的大小关系．
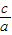，x1•x2=．根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+的值．（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 1 | 2 | 3 | … | |
| y | … | 5 | 2 | 1 | 2 | … |