题目内容
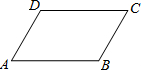如图在平行四边形ABCD中，∠B=2∠C，则∠D=________度，∠A=________度．
120 60
分析：根据平行四边形的性质可得出∠B+∠C=180°，结合∠B=2∠C，可得出∠B和∠C的度数，再由对角相等即可得出∠D和∠A的度数．
解答：∵四边形ABCD是平行四边形，
∴∠B+∠C=180°，∠D=∠B，∠A=∠C，
又∵∠B=2∠C，
∴∠B=120°，∠C=60°，
故可得∠D=∠B=120°，∠A=∠C=60°．
故答案为：120、60．
点评：此题考查了平行四边形的性质，属于基础题，掌握平行四边形的邻角互补、对角相等是解答本题的关键．
分析：根据平行四边形的性质可得出∠B+∠C=180°，结合∠B=2∠C，可得出∠B和∠C的度数，再由对角相等即可得出∠D和∠A的度数．
解答：∵四边形ABCD是平行四边形，
∴∠B+∠C=180°，∠D=∠B，∠A=∠C，
又∵∠B=2∠C，
∴∠B=120°，∠C=60°，
故可得∠D=∠B=120°，∠A=∠C=60°．
故答案为：120、60．
点评：此题考查了平行四边形的性质，属于基础题，掌握平行四边形的邻角互补、对角相等是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
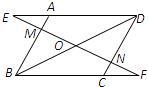21、已知：如图在平行四边形ABCD中，过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F．
7、如图在平行四边形ABCD中，如果AB=5，AD=9，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=
已知如图在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
如图在平行四边形ABCD中，AD=4cm，AB=2cm，则平行四边形ABCD的周长等于（ ）