题目内容
图①是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.
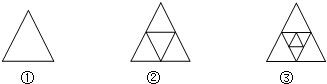
(1)图②有__________个三角形;图③有__________个三角形.
(2)按上面的方法继续下去,第5个图形中有__________个三角形;第n个图形中有__________个三角形?(用含有n的式子表示结论)
【考点】规律型:图形的变化类.
【专题】规律型.
【分析】(1)观察图形得到图①中三角形的个数为1,图②中三角形的个数为1+4,图③中三角形的个数为1+4×2;
(2)由(1)得到后面图形中的三角形个数比它前面它们的三角形个数多4,于是得到第n个图形中三角形的个数为1+4(n﹣1),则可计算出n=5时三角形的个数.
【解答】解:(1)图①中三角形的个数为1,
图②中三角形的个数为1+4=5,
图③中三角形的个数为1+4×2=9;
(2)图⑤中三角形的个数为1+4×4=17;
第n个图形中三角形的个数为1+4(n﹣1).
故答案为5,9;17;1+4(n﹣1).
【点评】本题考查了规律型﹣图形的变化类:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 3的倒数等于__________;
3的倒数等于__________; )×(﹣12)
)×(﹣12) B.
B. C.
C. D.
D.
 +
+ =
= B.
B. =
=
 =
= D.
D. =﹣
=﹣
 ,1),B(﹣2,3).
,1),B(﹣2,3).