题目内容

阅读下列材料：
∵

∴

解答问题：
（1）在式

中，第六项为，第

项为，上述求和的想法是通过逆用法则，将式中各分数转化为两个实数之差，使得除首末两项外的中间各项可以从而达到求和的目的．
（2）解方程

.

（1）

，分式的加减法，相互抵消。
（2）经检验x=－12和x=2为原方程的解解析:
本题主要考查分式的加减法

练习册系列答案

优优好卷单元测评卷系列答案

名校联盟快乐课堂系列答案

开心夺冠系列答案

同步测控全优设计系列答案

领航新课标练习册系列答案

培优大考卷系列答案

全程闯关100分系列答案

自主预习与评价系列答案

黄冈创优卷系列答案

佳分卷系列答案

相关题目

阅读下列材料并解答后面的问题：利用完全平方公式（a±b）²=a²±2ab+b²，通过配方可对a²+b²进行适当的变形，如a²+b²=（a+b）²-2ab或a²+b²=（a-b）²+2ab．从而使某些问题得到解决．例：已知a+b=5，ab=3，求a²+b²的值．
解：a²+b²=（a+b）²-2ab=5²-2×3=19．
问题：（1）已知a+

；
（2）已知a-b=2，ab=3，求a⁴+b⁴的值．

阅读下列材料：
为解方程（x²-1）²-5（x²-1）+4=0，我们可以将x²-1看作一个整体，设x²-1=y，则原方程可化为y²-5y+4=0，解得y₁=1，y₂=4．
当y₁=1时，x²-1=1，∴x=±

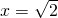；当y₂=4时，x²-1=4，∴x=±

．
因此原方程的解为：x1=

．
（1）已知方程

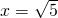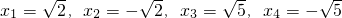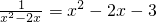=x2-2x-3，如果设x²-2x=y，那么原方程可化为

（写成关于y的一元二次方程的一般形式）．
（2）根据阅读材料，解方程：x（x+3）（x²+3x+2）=24．

请阅读下列材料：

为解方程(x²－1)²－5(x²－1)＋4＝0，我们可以将x²－1视为一个整体，然后设x²－1＝y，则原方程可化为y²－5y＋4＝0，①解得y₁＝1，y₂＝4．

当y＝1时，即x²－1＝1，解得x＝±；当y＝4时，即x²－1＝4，解得x＝±．

所以原方程的解共有四个：x₁＝，x₂＝－，x₃＝，x₄＝－．

请解答下列问题：

(1)由原方程得到方程①的过程中，运用换元的方法达到了________的目的，这是数学中转化思想的运用；

(2)运用这种方法解方程：(x²－2x)²－11(x²－2x)＋24＝0．

阅读下列材料：
为解方程（x²-1）²-5（x²-1）+4=0，我们可以将x²-1看作一个整体，设x²-1=y，则原方程可化为y²-5y+4=0，解得y₁=1，y₂=4．
当y₁=1时，x²-1=1，∴ $数学公式$ ；当y₂=4时，x²-1=4，∴ $数学公式$ ．
因此原方程的解为： $数学公式$ ．
（1）已知方程 $数学公式$ ，如果设x²-2x=y，那么原方程可化为________（写成关于y的一元二次方程的一般形式）．
（2）根据阅读材料，解方程：x（x+3）（x²+3x+2）=24．

阅读下列材料：
为解方程（x²-1）²-5（x²-1）+4=0，我们可以将x²-1看作一个整体，设x²-1=y，则原方程可化为y²-5y+4=0，解得y₁=1，y₂=4．
当y₁=1时，x²-1=1，∴

；当y₂=4时，x²-1=4，∴

．
因此原方程的解为：

．
（1）已知方程

，如果设x²-2x=y，那么原方程可化为______（写成关于y的一元二次方程的一般形式）．
（2）根据阅读材料，解方程：x（x+3）（x²+3x+2）=24．