题目内容
如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为 cm.(结果保留根号)
【答案】分析:首先根据题意作图,然后连接B′B″,由在Rt△ABC中,AB=12,∠A=30°,即可求得AC与BC的值,则可得AB′的值,又由B′C∥B″C″,B′C=B″C″,四边形B″C″CB′是矩形,可得△AB″B′∽△ABC,然后根据相似三角形的对应边成比例,即可求得答案.
解答: 解:如图:连接B′B″,
解:如图:连接B′B″,
∵在Rt△ABC中,AB=12,∠A=30°,
∴BC= AB=6,AC=6
AB=6,AC=6 ,
,
∴B′C=6,
∴AB′=AC-B′C=6 -6,
-6,
∵B′C∥B″C″,B′C=B″C″,
∴四边形B″C″CB′是矩形,
∴B″B′∥BC,B″B′=C″C,
∴△AB″B′∽△ABC,
∴ ,
,
即: ,
,
解得:B″B′=6-2 .
.
∴C″C=B″B′=6-2 .
.
故答案为:6-2 .
.
点评:此题考查了相似三角形的判定与性质,旋转与平移的性质,以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是数形结合思想的应用.
解答:
 解:如图:连接B′B″,
解:如图:连接B′B″,∵在Rt△ABC中,AB=12,∠A=30°,
∴BC=
 AB=6,AC=6
AB=6,AC=6 ,
,∴B′C=6,
∴AB′=AC-B′C=6
 -6,
-6,∵B′C∥B″C″,B′C=B″C″,
∴四边形B″C″CB′是矩形,
∴B″B′∥BC,B″B′=C″C,
∴△AB″B′∽△ABC,
∴
 ,
,即:
 ,
,解得:B″B′=6-2
 .
.∴C″C=B″B′=6-2
 .
.故答案为:6-2
 .
.点评:此题考查了相似三角形的判定与性质,旋转与平移的性质,以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
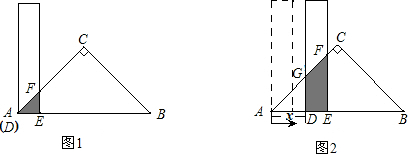
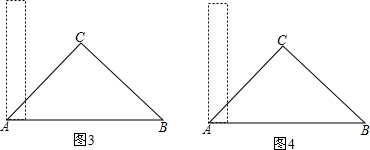
 (2013•杨浦区二模)如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为
(2013•杨浦区二模)如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为 如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为________cm.(结果保留根号)
如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为________cm.(结果保留根号)