题目内容
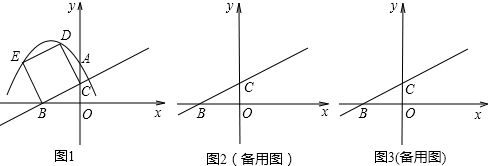
如图1,在直角坐标系中,已知点A(0,2)、点B(-2,0),过点B和线
段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
(1)填空:点D的坐标为( ),点E的坐标为( ).
(2)若抛物线 经过A、D、E三点,求该抛物线的解析式.
经过A、D、E三点,求该抛物线的解析式.
(3)若正方形和抛物线均以每秒 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E
落在y轴上时,正方形和抛物线均停止运动.
①在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,
并写出相应自变量t的取值范围.
②运动停止时,求抛物线的顶点坐标.
解:(1)D(-1,3),E(-3,2)。
(2)抛物线经过(0,2)、(-1,3)、(-3,2),则 ,解得
,解得  。
。
∴抛物线的解析式为
? (3)①求出端点的时间:
当点D运动到y轴上时,如图1,DD1= DC=
DC= BC =
BC = ,t=
,t= 。
。
当点B运动到y轴上时,如图2,BB1=BC= ,t=
,t= 。
。
当点E运动到y轴上时,如图2,EE1=ED+DE1= ,t=
,t= 。
。
当0<t≤ 时,如图4,正方形落在y轴右侧部分的面积为△CC′F的面积,设D′C′交y轴于点F。
时,如图4,正方形落在y轴右侧部分的面积为△CC′F的面积,设D′C′交y轴于点F。
∵tan∠BCO= =2,∠BCO=∠FCC′,
=2,∠BCO=∠FCC′,
∴tan∠FCC′="2," 即 =2。
=2。
∵CC′= t,∴FC′=2
t,∴FC′=2 t。
t。
∴S△CC′F?= CC′·FC′=
CC′·FC′= t×
t× t="5" t2。
t="5" t2。
当 <t≤1时,如图5,正方形落在y轴右侧部分的面积为直角梯形CC′D′G的面积,设D′E′交y轴于点G,过G作GH⊥B′C′于H。
<t≤1时,如图5,正方形落在y轴右侧部分的面积为直角梯形CC′D′G的面积,设D′E′交y轴于点G,过G作GH⊥B′C′于H。
∵GH=BC= ,∴CH=
,∴CH= GH=
GH= 。
。
∵CC′= t,∴HC′= GD′=
t,∴HC′= GD′= t-
t- 。
。
∴
当1<t≤ 时,如图6,正方形落在y轴右侧部分的面积为五边形B′C′D′MN的面积,设D′E′、E′B′分别交y轴于点M、N。
时,如图6,正方形落在y轴右侧部分的面积为五边形B′C′D′MN的面积,设D′E′、E′B′分别交y轴于点M、N。
∵CC′= t,B′C′=
t,B′C′= ,
,
∴CB′= t-
t- 。∴B′N=2CB′=
。∴B′N=2CB′= t-
t- 。
。
∵B′E′= ,∴E′N=B′E′-B′N=
,∴E′N=B′E′-B′N= -
- t。
t。
∴E′M= E′N=
E′N= (
( -
- t)。
t)。
∴ 。
。
∴ 。
。
综上所述,S与x的函数关系式为: 。
。
②当点E运动到点E′时,运动停止,如图7所示。
∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′,
∴△BOC∽△E′B′C。∴ 。
。
∵OB=2,B′E′=BC= ,∴
,∴ 。
。
∴CE′= 。
。
∴OE′=OC+CE′=1+ 。∴E′(0,
。∴E′(0, )。
)。
由点E(-3,2)运动到点E′(0, ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位。
个单位。
∵ ,∴原抛物线顶点坐标为(
,∴原抛物线顶点坐标为( )
)
?∴运动停止时,抛物线的顶点坐标为( )。
)。
解析

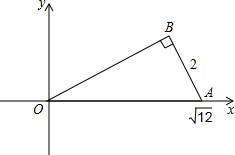 已知在Rt△OAB中,∠B=90°,
已知在Rt△OAB中,∠B=90°,
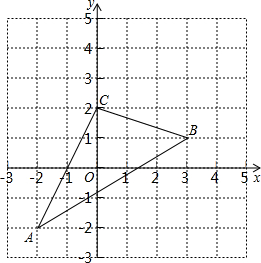 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,