题目内容
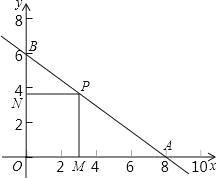
【题目】次函数的图象与x轴、y轴分别交于点A（8，0）和点B（0，6）．
（1）确定此一次函数的解析式．
（2）求坐标原点O到直线AB的距离．
（3）点P是线段AB上的一个动点，过点P作PM垂直于x轴于M，作PN垂直于y轴于N，记L=PM+PN，问L是否存在最大值和最小值？若存在，求出此时P点到原点O的距离，若不存在请说明理由．
【答案】(1)、y=﹣
x+6；(2)、4.8；(3)、当x=0时，L值最大，最大值为8，此时，点P到原点O的距离为8，x=8时，L值最小，最小值为6，此时，点P到原点O的距离为6．
【解析】
试题分析：(1)、设一次函数解析式为y=kx+b，把点A、B的坐标代入函数解析式，利用待定系数法求一次函数解析式解答；(2)、设点O到AB的距离为h，利用勾股定理列式求出AB，再利用△AOB的面积列式计算即可得解；(3)、设AM=x，表示出OM即PN的长，再利用∠BAO的正切值表示出PM，然后列出PM+PN的表达式，再根据一次函数的增减性求解即可．
试题解析：(1)、设一次函数解析式为y=kx+b， ∵函数图象经过点A（8，0）和点B（0，6），
∴
， 解得
． 所以，函数解析式为y=﹣
x+6；
(2)、设点O到AB的距离为h， ∵点A（8，0）和点B（0，6）， ∴OA=8，OB=6，
由勾股定理得，AB=
=
=10， S△AOB=
×10h=
×8×6， 解得h=4.8，
所以，坐标原点O到直线AB的距离为4.8；
(3)、设AM=x， 则OM=OA﹣AM=8﹣x， ∵PM⊥x轴，PN⊥y轴， ∴四边形OMPN是矩形，
∴PN=OM=8﹣x， ∵PM=AMtan∠BAO=
x=
x， ∴L=PM+PN=x+8﹣x=﹣
x+8，
∵点P是线段AB上的一个动点， ∴点M在线段OA上， ∴0≤x≤8， ∵﹣
＜0，
∴当x=0时，L值最大，最大值为8，此时，点P到原点O的距离为8，
x=8时，L值最小，最小值为6，此时，点P到原点O的距离为6．
