题目内容
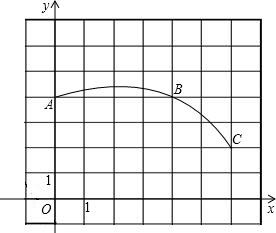
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1) 请在图中确定该圆弧所在圆心D点的位置,D点坐标为________;
(2) 连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3) 若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

解: (1)如图;D(2,0)
 (2)如图;
(2)如图;![]()
作CE⊥x轴,垂足为E.
∵△AOD≌△DEC
∴∠OAD=∠CDE
又∵∠OAD+∠ADO=90°
∴![]() ∠CD
∠CD![]() E+∠ADO=90°
E+∠ADO=90°
∴扇形DAC的圆心角为90度.
(3)方法一:
∵弧AC的长度即为圆锥底面圆的周长.
![]()
设圆锥底面圆半径为r,则
![]() ∴
∴![]()
方法二:圆锥的侧面积![]() ,其中母线l即为⊙D的半径
,其中母线l即为⊙D的半径![]() ;r为圆锥的底面半径. 又扇形DAC的面积:
;r为圆锥的底面半径. 又扇形DAC的面积:
![]()
∴ ![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
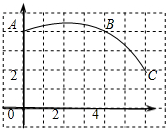 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作: