题目内容

点M是抛物线y=2（x-3）²-3的顶点，则点M关于x轴对称的点的坐标为

A.
（3，-3）
B.
（3，3）
C.
（-3，3）
D.
（-3，-3）

B
分析：根据所给二次函数的解析式可直接得出顶点M的坐标，再根据点关于x轴对称的特点可求M对称点的坐标．
解答：∵y=2（x-3）²-3，
∴M的坐标是（3，-3），
∴M关于x轴对称的点的坐标是（3，3），
故选B．
点评：本题考查了二次函数的性质，解题的关键是熟练掌握二次函数的各种表达式，以及坐标系内点的对称点的坐标的特点．

练习册系列答案

提分百分百检测卷系列答案

权威考卷系列答案

密码大考卷系列答案

宝贝计划期末冲刺夺100分系列答案

能考试全能100分系列答案

名师名校全能金卷系列答案

学效评估完全测试卷系列答案

赢在课堂全程优化达标测评卷系列答案

浙江期末冲刺100分系列答案

全能卷王评价卷系列答案

相关题目

如图，已知点P是抛物线y=

x2+1上的任意一点，记点P到X轴距离为d₁，点P与点F（

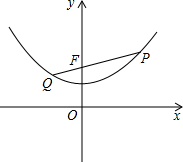0，2）的距离为d₂
（1）证明d₁=d₂；
（2）若直线PF交此抛物线于另一点Q（异于P点），试判断以PQ为直径的圆与x轴的位置关系，并说明理由．

如图，抛物线y=-

m2（m＞0）与x轴相交于A，B两点，点

H是抛物线的顶点，以AB为直径作圆G交y轴于E，F两点，EF=4

．
（1）用含m的代数式表示圆G的半径r_G的长；
（2）连接AH，求线段AH的长；
（3）点P是抛物线对称轴正半轴上的一点，且满足以P点为圆心的圆P与直线AH和圆G都相切，求点P的坐标．

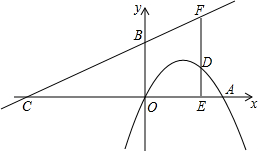如图，在平面直角坐标系中，抛物线y=-x²+bx经过A（2，0），直线y=

x+m分别交x轴、y轴于点C、B，点D是抛物线上横坐标为m的点，作DE⊥x轴于E，DE所在的直线与直线y=

x+m交于点F．
（1）求该抛物线解析式；
（2）随着m的变化，试探究：
①当m取何值时，点D和点F重合；
②当1＜m＜2时，用含m的代数式表示DF的长度；
（3）将DF绕D顺时针旋转90°得到DF′，连结E F′，是否存在△DE F′与△CEF相似？若有，请求出m的值；若没有，请说明理由．

如图1，抛物线y=ax²-5ax+4经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．
（1）求抛物线的解析式；

（2）若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形，若存在，求出所有符合条件的点P坐标；不存在，请说明理由；
（3）如图2，将△AOC沿x轴对折得到△AOC₁，再将△AOC₁绕平面内某点旋转180°后得△A₁O₁C₂（A，O，C1分别与点A₁，O₁，C₂对应）使点A₁，C₂在抛物线上，求A₁，C₂的坐标．

已知对称轴平行于y轴的抛物线经过点B（0，1），顶点是A（2，0），
（1）求这条抛物线的解析式；
（2）在抛物线上是否存在一点P，使以BP为直径的圆经过抛物线的顶点A？若不存在说明理由；若存在，求出符合条件的圆的直径长度；
（3）对于（2）中的点P，当△ABP能构成时，点M是抛物线上A、P之间的动点，求△BMP面积最大值．