题目内容
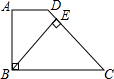 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BE⊥CD于点E,AD=1,CD=3
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BE⊥CD于点E,AD=1,CD=3| 2 |
2
| 2 |
2
.| 2 |
分析:首先过点D作DF⊥BC于点F,连接BD,利用等腰直角三角形的性质可得DF,FC的长,再利用三角形面积求法得出BE的长.
解答: 解:过点D作DF⊥BC于点F,连接BD,
解:过点D作DF⊥BC于点F,连接BD,
∵∠C=45°,
∴∠FDC=45°,
∴DF=FC,
∵CD=3
,
∴DF=CF=CDcos45°=
×3
=3,
∵AD=1,
∴BC=4,
∴
×DF×BC=
×BE×CD,
∴
×3×4=
BE×3
,
解得:BE=2
.
故答案为:2
.
 解:过点D作DF⊥BC于点F,连接BD,
解:过点D作DF⊥BC于点F,连接BD,∵∠C=45°,
∴∠FDC=45°,
∴DF=FC,
∵CD=3
| 2 |
∴DF=CF=CDcos45°=
| ||
| 2 |
| 2 |
∵AD=1,
∴BC=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
解得:BE=2
| 2 |
故答案为:2
| 2 |
点评:此题主要考查了直角梯形的性质以及三角形面积求法和锐角三角函数关系应用,根据已知得出DF,FC的长是解题关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
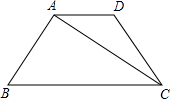 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.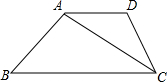 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,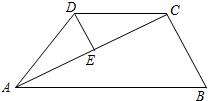 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=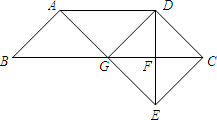 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.