题目内容
1.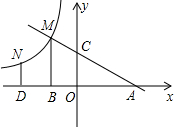 如图,直线y=-$\frac{1}{2}$x+2分别交x轴,y轴于A,C,M为第二象限内的一点,MB⊥x轴,B为垂足,S△ABM=9.
如图,直线y=-$\frac{1}{2}$x+2分别交x轴,y轴于A,C,M为第二象限内的一点,MB⊥x轴,B为垂足,S△ABM=9.(1)求点M的坐标;
(2)设点N与点M在同一个反比例函数的图象上,且点N在直线MB左侧交于x轴,D为垂足,当△BND∽△ACO时,求点N的坐标.
分析 (1)用一个未知数设出点M的坐标,表示出△AMC的面积,即可求得点M的坐标;
(2)设N坐标为(x,y),求出反比例函数,因为△BND∽△ACO,利用线段比联立方程组求出x,y的值.
解答 解:(1)∵点M在直线y=-$\frac{1}{2}$x+2上,
∴设M(x,-$\frac{1}{2}$x+2),
易得A(4,0),C(0,2)
∵S△ABM=9
∴$\frac{1}{2}AB•MB=9$,
∴$\frac{1}{2}(4-x)(-\frac{1}{2}x+2)=9$
解得:x1=-2,x2=10(舍去)
∴-$\frac{1}{2}$x+2=$-\frac{1}{2}×(-2)+2=3$
∴M(-2,3)
(2)如图①设N的坐标为(x,y),
M坐标为(-2,3)
∴经过M点的反比例函数解析式为y=$-\frac{6}{x}$(x<0),
又∵△BND∽△ACO,
∴①$\frac{OA}{OC}=\frac{BD}{ND}$时,有$\frac{4}{2}=\frac{-2-x}{y}$
则有$\left\{\begin{array}{l}{y=-\frac{6}{x}}\\{2y=-x-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=-1-\sqrt{13}}\\{y=\frac{\sqrt{13}-1}{2}}\end{array}\right.$
②$\frac{AO}{OC}=\frac{DN}{DB}$时,有$\frac{4}{2}=\frac{y}{-2-x}$
则有$\left\{\begin{array}{l}{y=-\frac{6}{x}}\\{y=-2x-4}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1}\\{y=-6}\end{array}\right.$(不在第二象限,舍去),或$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$
∴点n的坐标为$(-1-\sqrt{13},\frac{\sqrt{13}-1}{2})$或(-3,2).
点评 本题考查的是一次函数与反比例函数的综合运用以及相似三角形的判定,解题时首先根据一次函数解析式求出A、C两点的坐标,再由S△ABM=9求得点M的坐标,从而可得反比例函数解析式,最后根据相似三角形的判定和性质求出点N的坐标;本题综合性较强,难度中上.

 名校课堂系列答案
名校课堂系列答案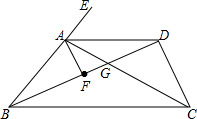 如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )
如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ① | D. | ②③ |
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
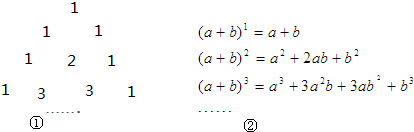

 如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )